L’algorithme de Peter Shor inventé en 1994 et qui permet de factoriser rapidement des nombres entiers secoue le monde de la sécurité informatique depuis au moins une bonne quinzaine d’années. En effet, il permet en théorie de casser les codes de nombre de systèmes de cryptographie à clés publiques qui sont couramment utilisés sur Internet.
Alors qu’il est loin d’être opérationnel à grande échelle du fait de l’absence d’ordinateurs quantiques universels avec un très grand nombre de qubits logiques, les services de contre-espionnage, de renseignement et les entreprises s’en inquiètent sérieusement lorsqu’ils sont au courant de la menace. Elle pèse même sur une partie du fonctionnement du Bitcoin et de la BlockChain !
Avant donc même que la menace fantôme de Shor se matérialise concrètement, l’industrie de la protection des communications et des contenus se met en ordre de bataille pour y faire face, et plus ou moins rapidement selon les parties prenantes. Les marchés touchés en premier seront l’industrie informatique et des télécoms en général qui va devoir mettre à jour de nombreuses offres logicielles si ce n’est matérielles, les banques, la distribution, la santé et les activités régaliennes des services publics.
Dans cette partie, nous allons décrire dans l’ordre :
- Les principes de base de la cryptographie, notamment à clé publique, avec l’exemple des clés publiques RSA.
- La menace provenant de la factorisation de nombres entiers et les solutions de cryptographie concernées.
- Les générateurs de nombres aléatoires quantiques, compléments devenus indispensables des solutions de cryptographie de haut vol.
- Les clés quantiques qui permettent de sécuriser la partie physique des communications pour l’usage de clés symétriques.
- La cryptographie post-quantique qui sert à protéger la partie logique des communications cryptées dans le cas de l’usage de clés publiques.
- Les startups et offres commerciales de ces secteurs dans le monde, dans un marché qui comprend déjà de nombreux acteurs.
Comme d’habitude, ce genre de post est le résultat d’une intense recherche bibliographique. Je n’invente rien ! Tout est là, prêt à être synthétisé. Je cite à chaque fois que possible les sources d’informations que j’utilise dans ce travail de vulgarisation. Ce sujet de la cryptographie avait la particularité de ne pas m’intéresser énormément. Mais pour que cette série soit bien complète et du fait des liens évidents avec le calcul quantique, j’ai décidé de le couvrir convenablement. A force de le creuser, j’ai trouvé le sujet intéressant !
Mais je me suis heurté à un domaine que les spécialistes ne vulgarisent vraiment pas bien du tout. C’est d’un cryptique, c’est le cas de le dire ! J’ai donc eu ici l’impression d’être encore plus largué que lorsque je m’attaquais au modèle de représentation mathématique des qubits, aux registres quantiques ou aux algorithmes quantiques. Je préfère le dire et l’assumer ! Sans vous décourager pour autant car ce que j’ai compris permet déjà se dégrossir le sujet à grosses mailles avant d’essayer de creuser les mathématiques associées si cela vous chante, ou si vous l’avez déjà fait.
Le principe de la cryptographie par clé publique
Côté vocabulaire, précisons que la cryptologie est la science des secrets. Elle permet la transmission d’informations sensibles entre un émetteur et un récepteur et de manière sure. La cryptologie comprend la cryptographie, qui sécurise l’information émise et la cryptanalyse qui cherche à la décrypter par attaque. Les puristes francophones parlent de chiffrement et de déchiffrement, lorsque l’on encode et décode l’information puis de décryptage, lorsqu’un attaquant décode les messages. Dans le cas de la cryptographie asymétrique à clé publique, le chiffrement n’exploite que les clés publiques et le déchiffrement s’appuie sur les clés publiques et privées. Le décryptage exploite uniquement les clés publiques en cherchant à en déduire les clés privées par du calcul, souvent intensif.
La cryptographie sécurise l’information transmise de plusieurs manières : par la confidentialité (seul le destinataire peut récupérer la version non cryptée de l’information transmise), par l’intégrité (l’information n’a pas été modifiée pendant sa transmission), par l’authentification (chacun est bien celui qu’il prétend être), la non-répudiation (l’émetteur ne peut pas nier avoir transmis l’information cryptée) et le contrôle d’accès (seuls les personnes autorisées par l’émetteur et le récipiendaire peuvent accéder à l’information non cryptée).
Avant les télécommunications informatiques, la confidentialité était assurée par la connaissance d’un secret commun entre émetteurs et récepteurs, les fameux codes de chiffrement et de déchiffrement, pouvant être la position des roues d’une machine Enigma allemande pendant la seconde guerre mondiale. Cela fonctionnait dans des environnements fermés comme pour les communications militaires ou entre ambassades et pays d’origine.
Avec les communications sur Internet, ce mode opératoire est inapplicable pour des applications grand public et pour les relations entre les entreprises en général. D’où les systèmes de cryptographie à clés publiques, notamment RSA, qui servent à un grand nombre d’échanges d’informations. Il subsiste des systèmes très protégés à base de clés privées et symétriques et qui sont principalement utilisés dans le cadre des applications régaliennes (armée, sécurité, renseignement) ainsi que dans divers autres cas (transferts de fichiers, chiffrage de mails, échanges serveur/client, dans les cartes à puces et terminaux de paiement associés).
La cryptographie asymétrique (à clés publique) est aussi exploitée pour l’établissement préalable de clés de chiffrement communes entre les utilisateurs de systèmes à clés privées, pour gérer l’intégrité des communications et pour l’authentification comme dans le protocole TLS sur Internet. Les informations sensibles sont alors cryptées avec ces clés et un algorithme symétrique type AES. AES est ainsi utilisé pour chiffrer les communications dans Whatsapp, Messenger et Telegram. Ces applications utilisent souvent également de la cryptographie asymétrique pour l’authentification, les échanges de clés et la gestion de l’intégrité des communications. Bref, dans de très nombreux cas, les systèmes de cryptographie symétriques cohabitent avec des systèmes de cryptographie asymétriques (à clés publiques). Bref, lorsque vous communiquez sur Internet de manière sécurisée, ce sont plusieurs protocoles de sécurité complémentaires qui sont activés.
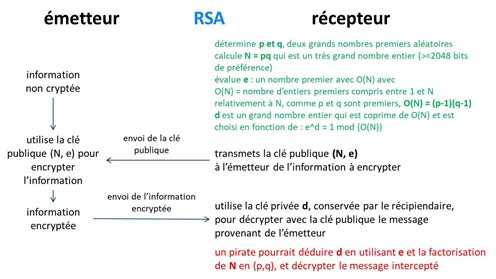
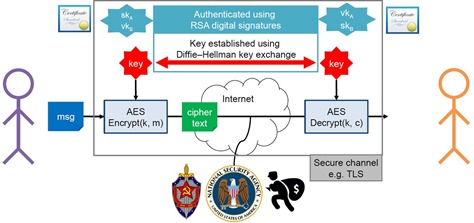
Dans les systèmes à clé publique, des clés différentes sont utilisées pour le chiffrement et le déchiffrement des informations transmises, de telle manière qu’il est très difficile (si ce n’est parfois impossible) de déduire la clé privée de déchiffrement à partir de la clé publique de chiffrement. C’est le récepteur du message qui envoie sa clé publique à l’émetteur, qui l’utilise à son tour pour chiffrer le message. Le récepteur utilise la clé privée qu’il a conservée pour déchiffrer le message reçu. Comme l’explique le schéma ci-dessus, la clé privée n’est jamais transmise. C’est ce que l’on appelle aussi une PKI, pour “Public Key Infrastructure”.
L’algorithme RSA est le plus connu et le plus utilisé des systèmes de protection des transmissions d’information par clé publique sur Internet. Il a été créé en 1978 par Ron Rivest (1947, Américain), Adi Shamir (1952, Israélien) et Leonard Adleman (1945, Américain).
Vous n’avez pas forcément besoin de comprendre la tambouille interne que voici et qui explique comment les clés sont construites. Cela commence par la détermination de p et q, deux grands nombres premiers aléatoires, avec un “bon” générateur de nombres aléatoires. Nous verrons plus loin que la physique quantique permet de créer des générateurs de nombres vraiment aléatoires. On calcule N = pq qui est un très grand nombre entier. Une bonne clé RSA requiert d’avoir N stocké sur au moins 2048 bits sachant que la NSA recommande des clés de 3072 bits pour les applications critiques.
On évalue ensuite e, un nombre premier en exploitant O(N) qui égale le nombre d’entiers premiers compris entre 1 et N relativement à N, et qui, comme p et q sont premiers, égale (p-1)(q-1). d est un grand nombre entier qui est copremier de O(N) et est choisi en fonction de : e^d = 1 mod (O(N)). A la fin, on obtient une clé publique qui comprend les entiers N et e, et une clé privée qui comprend d. L’ensemble s’appuie sur la théorie des nombres et utilise notamment le petit théorème de Fermat et le théorème d’Euler qui permettent de créer deux clés distinctes et inverses l’une de l’autre.
La beauté du système permet à n’importe qui d’encrypter un message à partir de la clé publique, ce message n’étant déchiffrable que par celui qui dispose de la clé privée qui décompose la clé publique en primitives.
Un pirate pourrait décrypter l’information envoyée en exploitant e (le bout de la clé publique) et en factorisant N, l’autre bout de la clé publique, en entiers p et q, puis en déduire la clé privée d. A ce jour, la factorisation de nombres premier demande une puissance machine traditionnelle qui croit à la vitesse de la racine carrée du nombre à factoriser. A ce jour, le record de factorisation officiel de clé RSA est de 768 bits, réalisé en 2010. Cela n’inventorie visiblement pas les records non communiqués de la NSA. Et il est recommandé d’utiliser des clés situées entre 1024 et 2048 bits !
La menace fantôme de Shor
Dans la partie de cette série dédiée aux algorithmes quantiques, nous avons décrit celui de Peter Shor inventé en 1994. C’est l’un des premiers algorithmes quantiques après celui de Deutsch-Jozsa dont nous avions vu qu’il ne servait quasiment à rien. L’algorithme de Shor a provoqué un intérêt pour le calcul quantique alors que les chercheurs n’avaient pas encore réussi à créer un seul qubit contrôlable par une porte quantique unitaire !
L’algorithme de Shor permet dans un temps raisonnable de factoriser des nombres entiers, proportionnel à leur logarithme. C’est donc une factorisation de temps linéaire en fonction du nombre de bits de la clé. Il se trouve que cela met à mal les systèmes de cryptographiques courants qui reposent sur la notion de clé publique.
Mais uniquement dans un futur relativement lointain ! En effet, pour factoriser un entier sur 1024 bits, il faudrait environ 166 millions de qubits universels avec un taux d’erreur de 0,1% ou 5,5 millions de qubits avec 0,01% d’erreur et 6,6 semaines de calcul à 1 MHz. Ce qui sera hors de portée des ordinateurs quantiques universels pour encore quelques années, au moins une dizaine.
Selon le NIST (National Institute of Standards and Technology US), il faudrait de 3000 à 5000 qubits logiques pour casser une clé RSA de 2048 bits. Selon les technologies utilisées, il faut multiplier ce chiffre par 200 à 20 000 pour le nombre de qubits physiques par qubits logiques, donc entre 1 million et 1 milliard de qubits physiques “universels”. Cela donne un peu de marge !
Une clé RSA de 762 bits proche du record de 2010 demanderait un ordinateur à recuit quantique du Canadien D-Wave avec 5,5 milliards de qubits, loin des 2048 existants selon High-fidelity adiabatic quantum computation using the intrinsic Hamiltonian of a spin system: Application to the experimental factorization of 291311, de Nike Dattani, Xinhua Peng et Jiangfeng Du, juin 2017 (6 pages). Ils évaluaient qu’un D-Wave de 5893 qubits pourrait faire l’affaire si tous les qubits étaient couplables de manière arbitraire, ce qui n’est pas possible du fait de la conception en matrice 2D des chipsets de D-Wave.
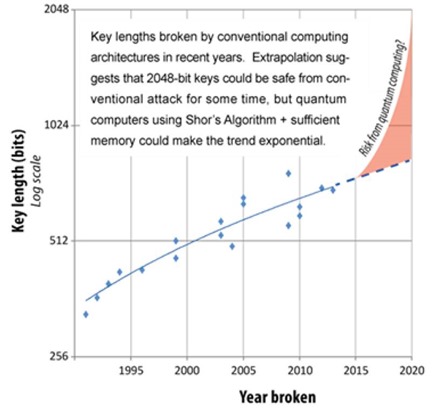
La menace de Shor est visualisée dans le temps dans ce schéma originaire de l’organisme de standardisation européen ETSI dont le siège est à Sophia-Antipolis, dans Quantum Safe Cryptography and Security, 2015 (64 pages). Elle s’appuie sur des prévisions très optimistes concernant les capacités des ordinateurs quantiques à exploiter l’algorithme de Shor. Il faudrait décaler vers le futur d’au moins 5 à 10 ans la partie orange du graphe.
La raison pour laquelle l’impact potentiel du quantique sur la cryptographie RSA est son large usage sur Internet. Il couvre les protocoles TLS et SSL qui protègent les sites web et les transferts de fichiers via FTP, le protocole IPSEC qui protège IP V4 dans le sous-protocole IKE, le protocole SSH d’accès à distance à une machine et PGP qui est parfois utilisé pour chiffrer les emails. La menace est encore plus large, au-delà de RSA. Elle couvrirait aussi la signature électronique de logiciels et donc leurs mises à jour automatiques, les VPN pour l’accès à distance aux réseaux d’entreprises protégés, la sécurisation des emails avec S/MIME, les systèmes de paiement, DSA (Digital Signature Algorithm, un protocole de signature électronique), Diffie-Hellman (pour l’envoi de clés symétriques) et la cryptographie à clés elliptiques ECDH, ECDSA et 3-DES. Le protocole Signal utilisé dans Whatsapp serait aussi en ligne de mire. Bref, une bonne part de la sécurité d’Internet est plus ou moins en ligne de mire.
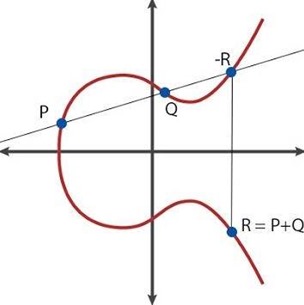
ECC (Elliptic Curve Cryptography) est le premier algorithme à courbes elliptiques, créé en 1985 par Neal Koblitz et Victor Miller. Les variantes les plus courantes d’aujourd’hui sont ECDH (Elliptic-curve Diffie–Hellman) et ECDSA (Elliptic Curve Digital Signature Algorithm, lancé en 2005). Ces variantes ont été déployées à partir de 2005 et plus largement seulement à partir de 2015, donc 30 ans après la création du premier ECC ! Au passage, les courbes elliptiques ont permis à Andrew Wiles de démontrer le dernier théorème de Fermat en 1992, qui n’a pas de rapports avec la cryptographie.
Je vous en passe les détails car je n’ai pas compris grand chose aux explications que j’ai pu trouver comme dans Elliptic curves cryptography and factorization (86 slides). Mas peu importe. L’un des intérêts des codes à base de courbes elliptiques est d’utiliser des clés publiques plus courtes qu’avec RSA. Mais voilà, ces courbes elliptiques sont aussi cassables en quantique avec un temps raisonnable à cause de notre ami Peter Shor, comme documenté dans Shor’s discrete logarithm quantum algorithm for elliptic curves, de John Proos and Christof Zalka, 2003 (34 pages). Qui plus est, une porte dérobée de l’ECDSA a été révélée par Edward Snowden en 2013, logée par la NSA dans son générateur de nombre aléatoire Dual EC DRBG. L’abandon de son usage était ensuite recommandé par le NIST en 2014 et la NSA en 2015 pour la transmission d’informations sensibles. Voir à ce sujet Elliptic Curve Cryptography and Government Backdoors de Ben Schwennesen, 2016 (20 pages).
La seconde raison est que des communications sensibles d’aujourd’hui peuvent être stockées par des pirates privés ou d’Etats, conservées et exploitées bien plus tard, le jour où les ordinateurs quantiques seront à la hauteur. Nombre d’informations d’aujourd’hui auront de la valeur plus tard, qu’ils s‘agisse de transactions financières, de communications privées diverses, de secrets industriels ou autres secrets d’Etats. Le calcul quantique est une véritable épée de Damoclès dont la chute est difficile à prévoir et plutôt éloignée dans le temps d’au moins une bonne décennie. Au-delà d’un tel délai, il est quasiment impossible de faire des prévisions.
Les systèmes de cryptographie symétriques ne sont pas concernés par l’algorithme de Shor. Il s’agit notamment du Data Encryption Standard (DES) qui utilise des clés de 64 bits ou plus et qui est dépassé, remplacé par l’Advanced Encryption Standard (AES) qui est un standard du gouvernement US depuis 2002, avec des clés privées allant de 128 à 256 bits. Les clés sont échangées en amont des échanges et généralement elles-mêmes chiffrées avec l’algorithme Diffie-Hellman (source du schéma ci-dessus). Les clés Diffie-Hellman sont cassables en quantique avec l’algorithme de Shor ! A ce jour, les meilleurs algorithmes de cassage quantique des clés AES mettraient plus que l’ancienneté de l’Univers (13,8 milliards d’années) pour s’exécuter sur des clés de 128 bits. Avec l’AES-256 bits, on est donc des plus tranquille !
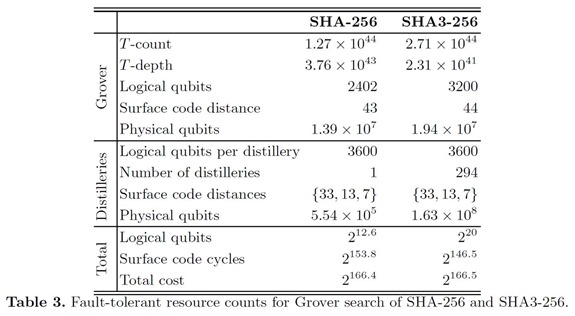
L’algorithme SHA-1 utilise aussi des clés symétriques résistantes à l’algorithme de Shor, mais il a été cassé par d’autres manières et est donc jugé dépassé. C’est le SHA-3 qui est le plus à jour et depuis 2015. D’après Estimating the cost of generic quantum pre-image attacks on SHA-2 and SHA-3, 2016 (21 pages), l’algorithme SHA peut être cassé par l’algorithme de recherche de Grover, mais avec une grande quantité de qubits, au minimum 6000 qubits logiques pour les clés courantes. Cela représente un ordre de grandeur voisin des besoins en qubits pour casser les clés RSA. Les algorithmes SHA (Secure Hash Algorithms) sont des standards de fonctions de hachage qui consistent à remplacer une donnée de taille arbitraire par une clé de taille unique. Une clé de hachage permet par exemple de vérifier l’intégrité d’un contenu comme un logiciel ou plus simplement, un mot de passe.
Le nombre de qubits nécessaires au cassage des clés dépend de la taille de la clé. SHA-1 et SHA-2 ont des tailles de clés faibles qui peuvent être récupérées en un temps considéré raisonnable avec l’algorithme quantique de recherche de Grover mais ce n’est pas le cas de SHA-3 qui exploite des clés plus grandes. C’est la même logique que pour AES.
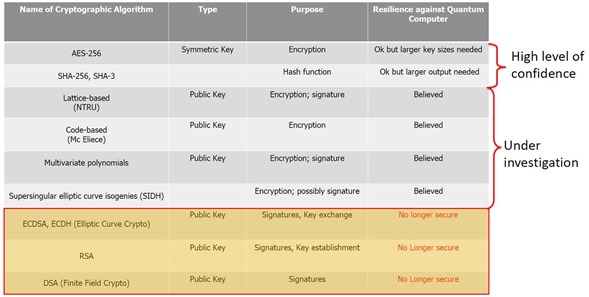
Le schéma ci-dessous pointe du doigt les algorithmes de cryptographie vulnérables au quantique, vu dans IDQ : Quantum-Safe Security elevance for Central Banks, 2018 (27 slides).
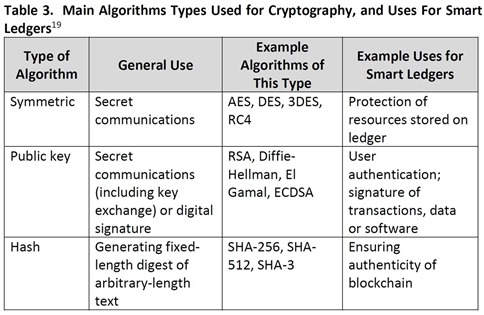
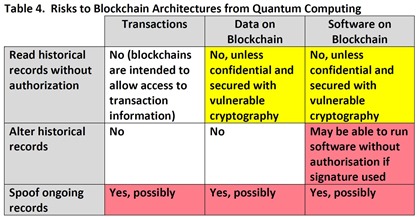
Qu’en est-il du Bitcoin, des crypto-monnaies et de la BlockChain ? J’ai trouvé une réponse fort bien documentée dans The Quantum Countdown Quantum Computing and The Future of Smart Ledger Encryption, de Long Finance, 2018 (60 pages) que je vous résume ci-dessous. Ils font pour commencer un bon inventaire des systèmes de cryptographie utilisés par usage.
En gros, la Blockchain s’appuie sur un patchwork d’algorithmes de cryptographie comprenant l’AES, RSA et SHA-3. Elle exploite un algorithme de hash pour s’assurer de l’intégrité de la chaine de confiance, et une signature numérique pour authentifier les nouvelles transactions qui s’ajoutent à la Blockchain de manière incrémentale. Dans le cas du Bitcoin, celui-ci utilise la crypto hash SHA-256 qui est résistante au quantique et une signature qui exploite des courbes elliptiques ECDSA qui elle ne l’est pas. Ethereum utilise un hash SHA-3 qui résiste au quantique et une signature ECDSA qui est vulnérable.
Au passage, rappelons qu’une fonction de hash converti une donnée de taille arbitraire comme un fichier en un nombre de taille fixe. Cela permet de faire des recherches rapides pour comparer des fichiers. Elle peut par exemple servir à vérifier qu’un fichier n’a pas été altéré pendant sa transmission.
Bref, le quantique ne permettra pas d’altérer la Blockchain ni la preuve de travail utilisée par le Bitcoin qui s’appuie sur l’usage répété de hash résistant au quantique. La vulnérabilité de la Blockchain se situe dans la signature qui s’appuie sur l’algorithme à courbes elliptiques ECDSA qui peut être cassée avec l’algorithme de Shor. Cela permettrait de se faire passer pour quelqu’un d’autre dans une transaction impliquant une Blockchain ou des Bitcoins.
Si une transaction Bitcoin était interceptée pour récupérer la signature ECDSA de l’émetteur, celle-ci pourrait être exploitée pour transférer des Bitcoins à partir du porte-monnaie de cet émetteur. Des solutions de contournement pourront évidemment être créées d’ici la confirmation d’une menace quantique sur l’intégrité des transactions. Il faudrait d’emblée encrypter les données d’une Blockchain avec un algorithme résistant au quantique comme AES-256, avec l’inconvénient qu’il est symétrique et nécessite donc que des clés soient échangées au préalable.
Il existe cependant déjà des parades. Un protocole utilisant un temps de validation plus long des transactions en Bitcoin permettrait de contourner l’usage de la factorisation d’entiers pour casser l’algorithme de signature électronique du Bitcoin, ECDSA. C’est documenté dans Committing to Quantum Resistance A Slow Defence for Bitcoin against a Fast Quantum Computing Attack, 2018 (18 pages). Mais cela ne ferait qu’amplifier un défaut clé du Bitcoin en tant que monnaie : un rallongement des temps de transaction qui est déjà loin d’être temps réel !
On peut aussi citer le projet open source de Blockchain résistante aux sournoises attaques du quantique : Quantum Resistant Ledger. Il s’appuie sur le protocole de signature électronique XMSS (Extended Merkle Signature Scheme).
Le document de Long Finance résume tous ces risques sur les Smart Ledgers en séparant les transactions qui sont relativement protégées et celles qui s’appuient sur des signatures électroniques vulnérables qui ne le sont pas. Il rappelle aussi que les échanges Internet sur lesquels s’appuient la Blockchain sont aussi vulnérables au hacking des protocoles SSL et TLS qui les protègent.
Pour en savoir plus, voir aussi The quantum threat to payment systems de Michele Mosca de l’Université de Waterloo, 2017 (52 minutes). Mosca est une des références mondiales du domaine.
Cette partie sur les menaces ne serait pas complète sans évoquer les désaccords qui règnent dans l’industrie et la recherche. Certains spécialistes de la cryptographie sont plutôt conservateurs et considèrent qu’il ne faut pas trop toucher à ce qui fonctionne bien. Ils pensent que l’on en fait trop avec la menace de Shor. D’autres, comme le NIST aux USA, sont plus alarmistes et sont d’avis qu’il ne faut pas tarder à mettre à jour les systèmes de cryptographie les plus critiques.
Génération de clés aléatoires quantiques
Nous allons maintenant passer à la description des trois briques de la cryptographie quantique avec pour commencer, la génération de clés aléatoires.
Les systèmes de cryptographie quantique et traditionnels sont tous alimentés par des générateurs de nombres aléatoires. Il en existe depuis des lustres. N’importe quel microprocesseur peut générer des nombres plus ou moins aléatoires. Le soucis des cryptographes est de disposer de nombres véritablement aléatoires. A savoir des suite de 0 et de 1 sans répétitions avec une proportion de 0 et de 1 équilibrée. Comme le sont les décimales du nombre pi ! Il faut de plus que la génération soit non déterministe et que l’on ne puisse pas la reproduire.
Une bonne part des générateurs de nombres aléatoires utilisés couramment sont pseudo-aléatoires et déterministes. Ce sont des PRNG, pour Pseudorandom Number Generators. On introduit de l’aléatoire en utilisant comme paramètres de l’algorithme de génération des éléments variables comme l’heure à la milliseconde près, les coordonnées GPS ou d’autres informations de contexte. Malheureusement, malgré ces variables d’initialisation, les algorithmes courants génèrent des périodes dans les nombres générés.
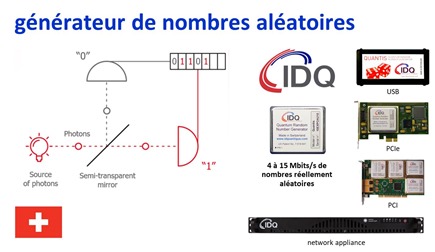
La solution consiste à utiliser un processus physique réellement aléatoire dans la génération de nombres. L’un des processus connus consiste à mesurer le bruit d’origine thermique d’un composant électronique comme dans un amplificateur. La méthode la plus aléatoire repose sur la physique quantique et en particulier sur un système conceptuellement assez simple reposant sur la mesure de la phase de photons émis individuellement en série. Voir Quantum Random Number Generators de Miguel Herrero-Collantes, 2016 (54 pages).
Elle permet de créer des nombres véritablement aléatoires de toute taille et assez rapidement, à raison d’un débit pouvant atteindre 1,5 Mbits aléatoires par seconde, voir même plusieurs dizaines de Gbits/s. Ils varient selon les processus utilisés. La technique est notamment maitrisée par la startup suisse IDQ ou ID Quantique, créée par le chercheur Nicolas Gisin, ainsi que par MagiQ, cryptomathic, Crypta Labs et PicoQuant.
Protéger les communications cryptées avec des clés quantiques
Nous l’avions déjà évoqué dans l’inventaire des scientifiques de la physique et de l’informatique quantique : en 1992, un certain Artur Ekert né en 1961, Polonais et Anglais, rencontre le physicien français Alain Aspect en 1992 pour lui soumettre l’idée d’utiliser l’intrication quantique de photons qu’il a vérifié dans son expérience en 1982 pour l’envoi de clés quantiques inviolables. Alain Aspect trouve l’idée intéressante. Artur Ekert venait de publier en 1991 l’article Quantum Cryptography Based on Bell’s Theorem (3 pages). ll est à l’origine du protocole E91 utilisant l’intrication quantique.
Elle a depuis fait son chemin. Elle est même à l’origine de la création du champ entier de la cryptographie quantique ! Artur Ekert fait partie depuis 2016 du conseil scientifique d’Atos en compagnie d’Alain Aspect, Daniel Estève, Serge Haroche, Cédric Villani et David DiVicenzo.
Le principe de base de la cryptographie quantique est celui de la QKD ou “quantum key distribution”. Il consiste à permettre l’échange de clés symétriques par voie optique (fibre optique, liaison aérienne ou satellite) en s’appuyant sur un système de protection de sa transmission contre les intrusions. Sa première mouture fut le protocole BB84 inventé par l’Américain Charles Bennett et le Canadien Gilles Brassard en 1984 dans Quantum cryptography : public key distribution and coin tossing, 5 pages. Ils sont les créateurs en 1982 de l’appellation de “cryptographie quantique”.
Artur Ekert a donc perfectionné BB84 en utilisant l’intrication quantique, évitant la transmission explicite d’information (de phase de photon) pouvant être interceptée par un intrus. La QKD a ensuite évolué, notamment avec le protocole BBM92 qui ajoute l’intrication au protocole BB84 et de manière plus sécurisée que le E91 de Artur Ekert. Il y a aussi le protocole CV-QKD pour “continuous variable”-QKD, qui module à la fois la phase et l’amplitude du signal optique transmis et permet notamment le multiplexage de plusieurs communications sur une même fibre optique.
Les protocoles de QKD ont la particularité de permettre la détection de toute intrusion dans la chaine de transmission et d’indiquer que quelqu’un a tenté d’en lire le contenu ou si des perturbations sont intervenues “sur la ligne”. Dans le protocole BB84, cela repose sur l’envoi de l’information sur des photons avec quatre types de phases : 0°, 45°, 90°, 135° et 180°. Histoire de faire simple car c’est en fait plus compliqué, leur lecture par un intrus va modifier leur phase, en rabattant leur polarisation à 0° ou 90°. Toute intrusion en lecture sera détectée à l’arrivée. Si le protocole détecte un intrus, il peut en tenir compte et bloquer la communication de l’information sensible parce que la clé d’encodage a été captée.
De son côté, l’information chiffrée avec la clé transmise est envoyée sur un canal traditionnel et en clair, même si elle est elle-même chiffrée généralement par des protocoles comme SSL qui protège les relations entre votre navigateur et les sites web que vous visitez et qui supportent Https. C’est d’ailleurs une modification que j’ai mise en place dans ce blog fin juillet 2018. Cela ne change pas grand chose dans la mesure où les lecteurs que vous êtes ne se connectent pas de manière sécurisée sur le site. Cela sécurise un peu mieux la connexion administrateur.
En pratique, la transmission de clé par QKD s’accompagne d’un système complexe de “distillation de clé” qui gère les imperfections de la communication avec des codes de correction d’erreurs, une amplification de la confidentialité et un système d’authentification par clés privées déjà partagées par les correspondants, permettant d’éviter les attaques “man in the middle” de pirates qui se feraient passer par l’un des interlocuteurs. Les codes de correction d’erreurs et le reste du protocole génèrent des pertes en ligne d’environ 80% de la communication des clés quantiques, selon l’excellent panorama de Sheila Cobourne de l’Université de Londres Quantum Key Distribution Protocols and Applications, 2011 (95 pages).
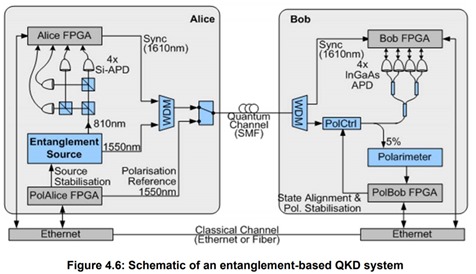
La mise en œuvre d’une QKD est encore complexe. On combine en général un générateur de clés aléatoire quantique comme ceux de Suisse IDQ, puis un système de génération de clé QKD logique, puis un encodage optique de cette clé qui va circuler généralement sur fibre optique. Séparément, le signal encrypté avec la clé (qui a été préalablement envoyée par la récipiendaire de l‘information s’il s’agit d’une clé publique) est envoyé sur un canal traditionnel, pouvant passer aussi par fibre optique ou un autre support de communication physique. C’est bien documenté dans Quantum Key Distribution (QKD) Components and Internal Interfaces de l’ETSI, 2018 (47 pages) qui décrit les différentes techniques de QKD disponibles à ce jour et d’où le schéma ci-dessus est issu.
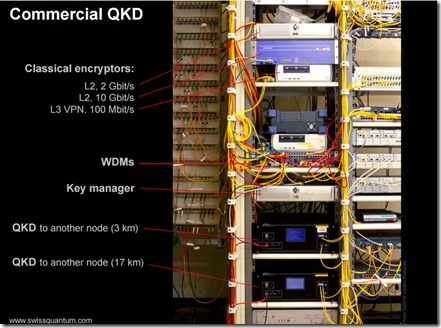
A l’arrivée, il faut le lecteur de clé quantique puis le système de déchiffrage du signal arrivé par voie normale. Cela donne pour l’instant de systèmes avec deux racks d’équipements comme en témoigne cette illustration ci-dessous issue de A tale of quantum computers de Alexandru Gheorghiu (131 slides).
Le canal protégé transportant la clé QKD peut cohabiter sur une même fibre optique avec le signal utile qui est transmis normalement et pour servir plusieurs utilisateurs simultanément, comme décrit dans Quantum Encrypted Signals on Multiuser Optical Fiber Networks Simulation Analysis of Next Generation Services and Technologies de l’Anglais Rameez Asif, 2017 (6 pages).
Les expériences symboliques de mise en œuvre de QKD se sont succédées ces dernières années. Les premières datent de 2005, menées par la DARPA à Boston. Une expérimentation a eu lieu à Vienne en 2008 dans le cadre du projet européen SECOQC (SEcure COmmunication based on Quantum Cryptography) lancé en 2004 et associant une quarantaine de laboratoires de recherche et d’entreprises privées, en exploitant une architecture “mesh”. Un test de liaison sur 144 km a été mené par des Autrichiens en 2010 pour relier les iles de La Palma et Tenerife aux Canaries, en utilisant le protocole BBM92, et documenté dans Feasibility of 300 km Quantum Key Distribution with Entangled States, 2010 (14 pages). Cela a continué en Suisse avec IDQ pour relier entre elles des banques locales.
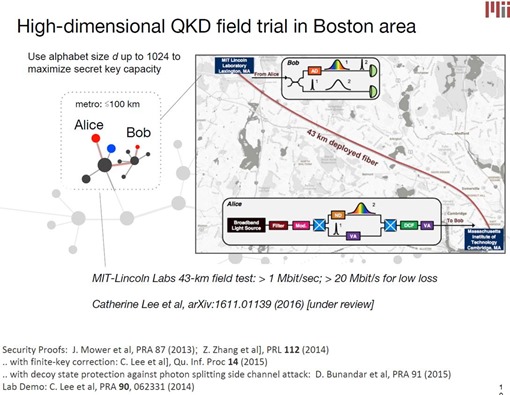
Les USA s’y sont également mis pour déployer un réseau inter-états de communication par QKD, piloté par Batelle (source). Des tests avaient déjà été réalisés en 2015 au MIT pour relier entre eux deux sites distants de 43 km (schéma ci-dessous issu de From MIT : Semiconductor Quantum Technologies for Communications and Computing, 2017, 32 slides), un type d’expérience aussi réalisée au Royaume Uni, vue dans IDQ : Quantum-Safe Security elevance for Central Banks, 2018 (27 slides) et leur UK Quantum Communications hub entre Bristol et Londres/Cambridge.
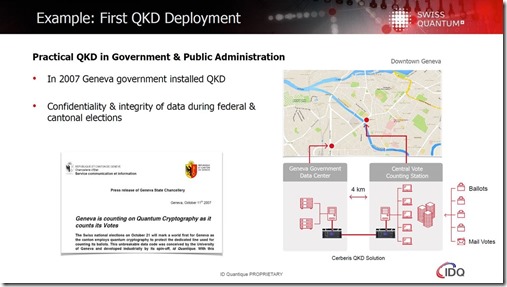
Cette même présentation évoque un système de décompte de votes d’élections s’appuyant sur une QKD (ci-dessous). Si les machines à voter sont elles-mêmes sécurisées, cela peut avoir un intérêt. Sinon, bien non ! La sécurité doit être de bout en bout !
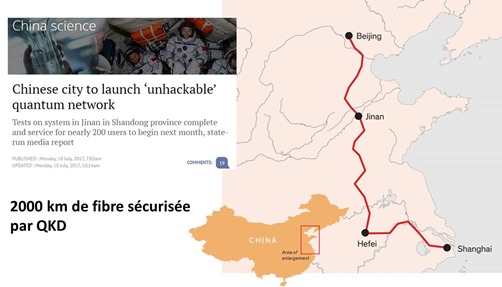
Ce sont les Chinois qui se font le plus remarquer avec des démonstrations et projets destinés à marquer les esprits. Comme nombre de pays, la Chine investit dans les QKD pour des raisons de souveraineté et pour protéger ses communications sensibles. Un premier déploiement avait été réalisé en 2012 dans la zone d’Hefei pour relier diverses entités du gouvernement chinois (source). Il a eu ensuite la mise en place d’une liaison par fibre optique sécurisée par QKD entre Shanghaï et Beiking, faisant 2000 km. Le projet lancé en 2016 et déployé par la startup chinoise QuantumCTek serait terminé. Sachant que sur 2000 km, il faut installer environ environ 25 répéteurs et en sécuriser l’accès physique ! En effet, l’atténuation du signal est trop forte au-delà d’environ 80 km sur une fibre optique.
La seconde performance chinoise concerne l’usage du satellite Micius pour téléporter des états quantiques de photons par voie optique en 2017, à 1400 km de distance entre la Terre (en altitude dans le Tibet) et le satellite. Les détails sont dans Ground-to-satellite quantum teleportation, 2017 (16 pages). Le principe a été décrit pour la première fois en 1993 dans Teleporting an Unknown Quantum State via Dual Classical and EPR Channels de Charles Bennett, Gilles Brassard (de Montréal), Claude Crépeau (un français de Normale Sup), Richard Jozsa, Asher Peres et William Wootters. Une communication de clé quantique QKD ensuite été réalisée, en utilisant un procédé différent, en 2018, entre la Chine et l’Autriche pour mener une vidéo-conférence sécurisée par cette clé (ci-dessous).
Qu’en est-il donc des répéteurs, indispensables pour distribuer des clés quantiques sur de grandes distances, au-delà de 80 km ? Des chercheurs chinois ont créé une connexion en fibre en QKD de 404 km sans répéteur, documentée dans Measurement device independent quantum key distribution over 404 km optical fibre, 2016 (15 pages), mais à cette distance les taux d’erreurs sont tellement élevés que cela ne sert par à grand chose. Il existe des technologies de répéteurs quantiques pour fibres optiques mais avec quelques limitations. On en serait déjà à la troisième génération de ces répéteurs mais ils seraient déjà hackables, selon The network impact of hijacking a quantum repeater 2018 (23 pages). Bref, ce n’est pas encore au point !
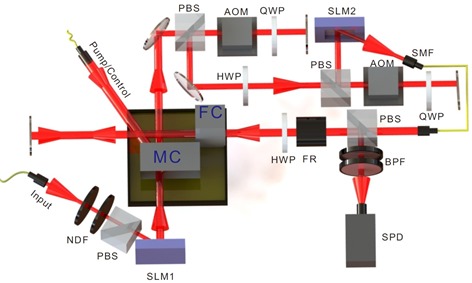
Une technique plus sûre consisterait à utiliser une mémoire quantique dans les répéteurs pour répliquer l’état des photons à transmettre. C’est l’objet de travaux de l’équipe de Nicolas Gisin de l’Université de Genève (et ID Quantique) accompagné d’une équipe du CNRS en France. Ils s’appuient sur une terre rare, l’ytterbium, selon Ytterbium: The quantum memory of tomorrow, juillet 2018. Ce n’est pas encore commercialisé. Dans la même veine, des chercheurs du Key Lab of Quantum Information de l’Académie des Sciences chinoise (lien) publiaient en août 2018 une étude sur la création de mémoires quantiques à base d’ions de terre rare (non précisé) dopés à trois degrés de liberté, pilotable par envoi de photons (schéma de l’expérience ci-dessous qui illustre le fait que l’on est encore loin de la miniaturisation). Cette technique pourrait servir à la fois à la création de répéteurs pour des réseaux de QKD et pour créer des mémoires quantiques pour ordinateurs quantiques à base d’optique linéaire.
La sécurisation d’une chaine dépend de ses maillons les plus faibles et ici, ce sont les émetteurs et les récepteurs avant même qu’ils n’échangent via une QKD. Par ailleurs, les QKD ne sont pas la panacée car elles dépendent d’une liaison point à point et pas d’une technique de routage permettant d’emprunter plusieurs chemins. Cela pourrait aboutir à une forme de déni de service par blocage de la communication physique employée.
Autre exemple, ce projet d’utiliser les QKD pour sécuriser une Blockchain. C’est évidemment délicat à déployer de bout en bout à grande échelle. En effet, les utilisateurs de Blockchain n’ont pas une liaison satellite en montagne ou une fibre sécurisée sous la main, ne serait-ce que lorsqu’ils sont mobiles. Mais soit. C’est la proposition de Evgeny Kiktenko du “Russian Quantum Center” de Moscou, documenté dans First Quantum-Secured Blockchain Technology Tested in Moscow, juin 2017 ainsi que de Del Rajan et Matt Visser de l’Université Victoria de Wellington en Nouvelle Zélande dans Quantum Blockchain using entanglement in time, 2018 (5 pages). Au juste, pourquoi ne protège-t-on pas l’ensemble des données transmises avec le même principe que la QKD ? Ce qui s’y oppose semble être la limitation en débit du procédé.
La cryptographie est fascinante pour la vitesse à laquelle des dispositifs de sécurité peuvent être cassés par des chercheurs avant même d’avoir été déployés en masse. Ainsi les QKD seraient vulnérables du fait d’une faille du théorème de Bell, comme le documente Jonathan Jogenfors dans Breaking the Unbreakable Exploiting Loopholes in Bell’s Theorem to Hack Quantum Cryptography 2017, (254 pages). C’est une course sans fin !
La cryptographie post-quantique
La protection physique de l’envoi de clés symétriques n’est pas facilement applicable de manière généralisée, ne serait-ce parce qu’elle impose une liaison optique (directe ou par fibre optique) entre émetteurs et récepteurs. Ce qui, par exemple, ne fonctionne pas avec les liaisons radio comme avec les smartphones. Too bad !
L’objectif que se sont donnés les spécialistes est donc de créer et exploiter des systèmes capables de résister aux assauts des ordinateurs quantiques et en particulier à l’algorithme de Shor (factorisation d’entiers mais aussi logarithme discret) comme de Grover (recherche brute) sans protection quantique de la liaison physique. Le décryptage de messages chiffrés – sans les clés privées – doit être un problème NP-Complet ou NP-Difficile pour résister aux assauts futurs du quantique.
Bref, la Post-Quantum Cryptography (PQC) est en quelque sorte concurrente de la Quantum Key Distribution (QKD) ! Et elle est certainement plus facile à déployer à grande échelle car elle est indépendante des infrastructures physiques utilisées pour les télécommunications.
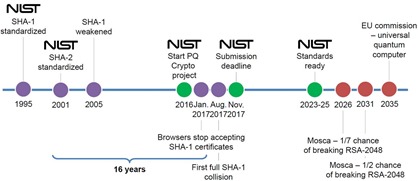
La chronologie mérite le détour pour sa dimension “long terme” sachant que j’en ai extrait un bout dans Quantum cryptanalysis – the catastrophe we know and don’t know de Tanja Lange, une des spécialistes du sujet et chercheuse aux Pays Bas, 2017 (33 slides) :
- 1978 : le premier algorithme résistant aux ordinateurs quantiques est créé par l’Américain Robert McEliece (détails plus loin) avant même que l’on parle d’ordinateurs quantiques.
- 2003 : Le terme de “post quantum cryptographie” (PQC) est créé par l’Américain Daniel Bernstein. C’est l’auteur avec Johannes Buchmann et Erik Dahmen de l’imposant ouvrage Post-Quantum Cryptography en 2009 (254 pages) qui pose bien les enjeux de la PQC.
- 2006 : le premier workshop international PQCrypto se tient en mai en Belgique pour étudier les moyens de contourner les attaques d’ordinateurs quantiques à une époque où l’on peut à peine faire fonctionner deux qubits ensemble. Le programme consiste à trouver des successeurs aux algorithmes de cryptographie à clés publique RSA et ECC qui résistent au quantique. Les actes sont ici : https://postquantum.cr.yp.to/pqcrypto2006record.pdf. Le comité de programme de 12 personnes comprend trois français : Louis Goubin de Université de Versailles ainsi que Phong Nguyen et Christopher Wolf de l’ENS. Dès cette première édition, quatre des cinq piliers de la PQC sont établis avec la code-based crypto, les lattice codes, hash Lamport signature et multivariate cryptography. Les isogénies arriveront plus tard. Deux français interviennent pour proposer deux de ces quatre pistes : Nicolas Sendrier, de l’INRIA, avec “Post-quantum code-based cryptography” et Jacques Stern de l’ENS avec “Post-quantum multivariate-quadratic public key schemes.”. Source : Quantum Computing and Cryptography Today de Travis L. Swaim, University of Maryland University College (22 pages). Ces workshops ont depuis lieu tous les ans à deux ans un peu partout dans le monde. L’édition 2013 avait eu lieu à Limoges.
- 2012 : le NIST (National Institute for Standards & Technologies), qui est une d’équivalent de l’AFNOR française, lançait ses premiers projets et une équipe sur la PQC.
- 2014 : l’Union Européenne lançait un appel à projets dans le cadre d’Horizon 2020 sur la PQC. Au même moment, l’ETSI qui est l’organisme européen de standardisation des télécoms, lançait aussi son groupe de travail sur la PQC.
- 2015 : le NIST organise son premier workshop sur la PQC. L’ETSI publie un document de référence sur la PQC, Quantum Safe Cryptography and Security (64 pages). La NSA se réveille un peu tardivement et déclare que le passage à la PQC va devenir une priorité dans Commercial national security algorithm suite and quantum computing FAQ IAD (11 pages). La NSA joue à chaque fois dans deux cours : elle veut se protéger et protéger les communications sensibles de l’Etat US avec de bons systèmes de chiffrement mais en même temps conserver des capacités à décrypter les communications commerciales standards et celles des autres pays. Cela repose sur la force brute de supercalculateurs géants et une forte asymétrie de moyens techniques. Cette asymétrie pourrait très bien disparaître avec les ordinateurs quantiques qui, sommes-toutes, seront peut-être bien plus abordables que les supercalculateurs géants. En 2015, le projet Européen PQCrypto coordonné par Tanja Lange est lancé. Il est documenté dans Post-Quantum Cryptography for Long-Term Security (10 pages).
- 2016 : le NIST publie un rapport d’étape sur la PQC (15 pages) et une roadmap de standardisation associée. Lancement du programme d’Investissement d’Avenir RISQ (Regroupement de l’Industrie française pour la Sécurité Post – Quantique) qui comprend outre divers laboratoires (CEA, CNRS, INRIA, UMPC), des entreprises privées comme CryptoExperts, CS, Secure-IC et Thalès. Ils ont fait des soumissions de propositions de standards au NIST en 2017. RISQ est piloté par Secure-IC.
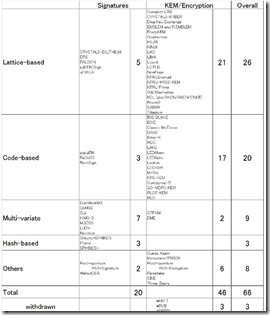
- 2017 : fin des soumissions de propositions de standardisation de PQC au NIST qui sont une quarantaine, concentrés dans les catégories des réseaux euclidiens et des codes linéaires aléatoires. 8eme workshop PQCrypto à Utrecht aux Pays-Bas.
- 2025 : c’est l’échéance que s’est donné le NIST pour finaliser les standards de la PQC aux USA (source de la timeline ci-dessous).
Quels sont au juste donc les standards en lice de la PQC ? Il sont dans cinq catégories distinctes que voici. Je ne vais pas pouvoir les décrire convenablement dans leur dimension mathématique sauf pour la première catégorie.
Code-based cryptography (EN) ou codes linéaires aléatoires (FR)
Ce système de cryptographie inventé en 1978 par Robert McEliece, bien avant l’existence de la menace de l’algorithme de Shor, a résisté depuis à toutes les attaques de cryptanalyse, soit classiques soit conçues avec des algorithmes quantiques. C’est le plus ancien des codes PQC qui était même “PQC” avant l’heure.
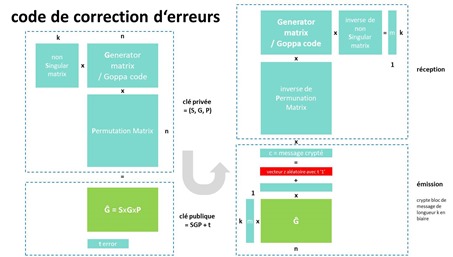
La méthode consiste à multiplier les données à encrypter représentées sous forme de vecteurs binaires par une matrice publique et statique avec plus de colonnes que de lignes, elle aussi binaire qui est un “code de Goppa binaire”. Allons donc. Cette multiplication génère un vecteur plus grand que le vecteur d’origine. On lui ajoute ensuite un vecteur binaire qui ajoute des erreurs aléatoires au résultat mais de nombre constant. Les spécialistes le décrivent comme un “uniformly random word of weight t” ce qui n‘est pas bien clair pour le néophyte, et qui fournit un exemple de plus du manque de pédagogie de certains. En langage un peu plus naturel, il s’agit d’une série de bits aléatoire contenant un nombre fixe “t” de 1 que l’on appelle le poids de Hamming.
La clé publique envoyée par le récepteur à l’émetteur est la matrice et ce nombre d’erreurs t. Ce sont les composantes génératrices de la matrice qui constituent la clé privée. En effet, cette matrice est la multiplication de trois matrices dites SGP pour “non singular”, “generator matrix / Goppa code” et “permutation matrix”. Le décodage du message utilise des inverses de la matrice S et de la matrice P, et la matrice G. C’est assez alambiqué et j’ai essayé de représenter cela graphiquement dans le schéma ci-dessus. La matrice G permet de supprimer les “t” erreurs introduites dans la phase de chiffrement. Elle est conçue pour cela au moment de la création des clés. Par contre, allez comprendre dans la phase d’émission l’effet mathématique de cette matrice de correction d’erreur au message à transmettre avant l’ajout de la dite erreur !
Ce système génère des clés publiques cent fois plus grande qu’avec RSA, de l’ordre de 80 Ko. Et si on réduire leur taille, cela génère des vulnérabilités. L’avantage est une bonne vitesse de chiffrement et de déchiffrement des messages. On peut même l’accélérer en utilisant un composant électronique dédié de type FPGA comme vu dans Code-Based Cryptography for FPGAs de Ruben Niederhagen, 2018 (73 slides).
Casser ce genre de chiffrement est un problème NP-Hard (NP-dur) inaccessible au quantique à ce jour même si, pour résister au quantique, il faudrait une clé assez grande, de 1 Mo. La résistance de cette méthode aux attaques est documentée dans Code-Based Cryptography de Tanja Lange, 2016 (38 slides).
Pour en savoir plus, voir aussi Code Based Cryptography d’Alain Couvreur, 2018 (122 slides) et Some Notes on Code-Based Cryptography, une thèse de Carl Löndahl, 2014 (192 pages).
Lattice-based cryptography (EN) ou réseaux euclidiens (FR)
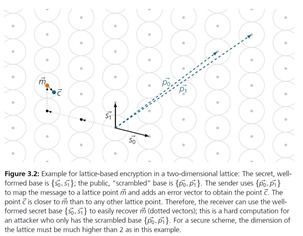
La technique a été proposée par le Hongrois Miklos Ajtai, chercheur chez IBM, en 1996, mise en œuvre dans un système à base de clé publique en 2005 par Oded Regev avec son système LWE (Learning with errors) et améliorée depuis par de nombreux chercheurs. La littérature sur le sujet est complètement inabordable pour les non spécialistes. Il n’est pas évident de comprendre le fonctionnement de cette méthode de chiffrement malgré l’élégance des schémas qui présentent la notion de réseau euclidien (ci-dessous). En gros, c’est une matrice de points qui permet de repérer des points en fonction de leurs coordonnées selon un repère de vecteurs différents entre la clé publique et la clé privée. Une erreur est ajoutée aux coordonnées générées avec le vecteur de la clé publique. Seuls les vecteurs de coordonnées de la clé privée permettent de retrouver la coordonnée de la valeur chiffrée. Bon, c’est ce que j’ai compris !
Initialement, elle souffrait de problèmes de performances mais des solutions efficaces sont apparues comme NTRU, créé en 1998 par Jeffrey Hoffstein, Jill Pipher et Joseph Silverman. L’avantage de la méthode est d’utiliser des clés publiques de petite taille. Son décryptage est un problème NP-complet inaccessible aux ordinateurs quantiques. Dans les inconvénients, c’est une méthode protégée par de nombreux brevets, donc propriétaire et potentiellement couteuse.
Pour en savoir plus, voir la thèse Lattice-based cryptography : a practical implementation, de Michael Rose, 2011 (103 pages), Lattice-based Cryptography de Daniele Micciancio et Oded Regev, 2008 (33 pages) et le tantinet plus pédagogique mais tout de même incompréhensible Overview of Lattice based Cryptography from Geometric de Leo Ducas, 2017 (53 slides).
Isogeny-based cryptography (EN) ou isogénie (FR)
Cette variante des courbes elliptiques est encore moins facile à appréhender que tout ce qui précède. En français, c’est un “morphisme de groupe surjectif et de noyau fini entre deux courbes elliptiques.”. Fastoche ! Le système a été proposé en 2006 par Alexander Rostovtsev et Anton Stolbunov puis cassé par cryptoanalyse quantique par Andrew Childs, David Jao et Vladimir Soukharev. Ce qui a conduit David Jao et Luca de Feo (INRIA) à proposer en 2011 l’utilisation de courbes “super-singulières” pour corriger cette faille.
Pour en savoir plus si le cœur vous en dit, voir 20 years of isogeny-based cryptography de Luca De Feo, 2017 (84 slides), An introduction to supersingular isogeny-based cryptography, de Craig Costello (Microsoft Research), 2017 (78 slides), Isogeny Graphs in Cryptography de Luca De Feo, 2018 (73 slides) ou encore An introduction to isogeny-based crypto de Chloe Martindale, 2017 (78 slides).
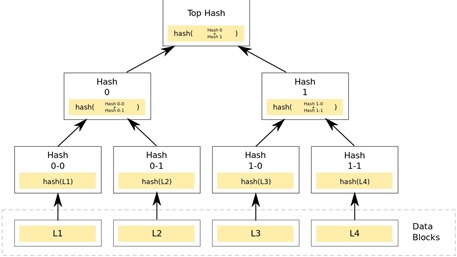
Hash-based signatures (EN) ou arbres de hashage (FR)
Cette autre méthode de cryptographie post-quantique est aussi antérieure à la notion même d’ordinateur quantique imaginée par Richard Feynman en 1982, puisqu’elle repose sur les travaux de Leslie Lamport du SRI en 1979 et ses “signatures” à base de hash à usage unique. La méthode a été ensuite améliorée en utilisant des arbres de hashage aussi appelé arbres de Merkle pour signer plusieurs messages. Le tout s’appuie sur des clés publiques de taille réduite, descendant à 1 kbits. Cette méthode est surtout utilisée pour de la signature électronique.
Pour en savoir plus si vous êtes un crack des maths et de la crypto, voir notamment Hash-based Signatures: An Outline for a New Standard (12 pages), Design and implementation of a post-quantum hash-based cryptographic signature scheme de Guillaume Endignoux, 2017 (102 pages) et SPHINCS: practical stateless hash-based signatures, 2015 (30 pages).
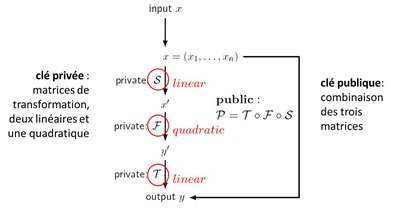
Multivariate polynomial cryptography (EN) ou inversion de polynômes multivariés (FR)
Ce dernier groupe de méthodes fait penser aux codes de correction d’erreurs. La clé publique est une multiplication de plusieurs matrices dont deux sont linéaires et une quadratique (avec des valeurs au carré), les trois matrices séparées constituant la clé privée qui sert à reconstituer le message chiffré. Le décryptage (donc, par des pirates) est un problème NP-Difficile, hors de portée des ordinateurs quantiques, sinon la méthode ne ferait pas partie de cet inventaire, pardi. La méthode date de 2009 et a évidemment été ensuite déclinée sous plusieurs variantes.
Les clés publiques sont assez grandes, allant par exemple jusqu’à130 Ko (avec la variante HFEBoost). A noter la contribution de Jacques Stern de l’ENS “Post-quantum multivariate-quadratic public key schemes” lors de PQCRYPTO 2006. A noter que cette méthode de chiffrement est plutôt utilisée pour les signatures électroniques.
En préparant cette partie, j’imaginais que l’on pouvait combiner de la QKD (protection physique de la distribution de clés) et de la PQC (protection logique du chiffrement contre le décryptage par ordinateur quantique). Et bien, pas vraiment. La QKD est plutôt dédiée aux algorithmes à clés symétriques qui supposent une protection de la communication physique entre correspondants tandis que la PQC s’appuie sur des clés publiques qui n’ont donc pas besoin d’être protégées par QKD car leur interception (sans la QKD) ne servirait déjà à rien à des pirates. On peut cependant combiner de la QKD pour l’échange de clés avec de la cryptographie post-quantique pour l’authentification et le chiffrement des données. La QKD a besoin d’authentification qui peut être assurée en amont par de la PQC. Par contre, la QKD peut être redondante avec de la PQC utilisée pour l’échange de clés.
Pour en savoir plus sur la PQC, voir notamment Post-quantum cryptography – dealing with the fallout of physics success de Daniel Bernstein et Tanja Lange, 2017 (20 pages), Post-Quantum Cryptography de Thomas Pöppelmann (Infineon), 2017 (32 slides), Le grand défi du post-quantique de Jean-Charles Faugère, 2018.
Les startups de la cryptographie quantique
Passons maintenant en revue les startups de ce vaste secteur d’activité de la cryptographie quantique et post-quantique, en essayant de bien décrire la nature de leur offre et de leur différenciation lorsque l’information est publiquement disponible ! Je n’ai conservé ici que les startups proposant des solutions technologies et pas intégré les sociétés de conseil et d’intégration.
AgilePQ (2014, USA) fournit une plateforme logicielle de sécurisation “post-quantum” de la communication entre objets connectés et le cloud, comme des drones. Il comprend AgilePQ C-code un bout de logiciel qui fonctionne sur les micro-contrôleurs d’objets connectés et consomme peu d’énergie et de l’autre, AgilePQ DEFEND, un système de génération de clé de taille adaptable. DEFEND génère des codes qui sont plus difficiles à casser que l’AES 256 et avec 429 ordres de grandeur de différence. Précisément, on passe d’un espace de clés de 10 puissance 77 à 8*10 puissance 506 (factorielle de 256), comme décrit dans AgilePQ DEFEND Cryptographic Tests (11 pages). Le système qui est breveté semble être une variante de codes linéaires aléatoires mais avec des clés de taille raisonnable. Il a été soumis à la standardisation au NIST et s’interface avec les systèmes de contrôle et de supervision SCADA (Supervisory control and data acquisition). La société est partenaire de Microsoft Azure. Pour une startup, ses dirigeants et fondateurs n’ont pas l’air bien jeunes, mais ils ont de l’expérience !
Citypassenger (France) est un intégrateur dans la sécurité qui a développé une solution de CV-QKD en partenariat avec la startup française SeQureNet (qui a visiblement mis la clé sous la porte en 2017) et Telecom ParisTech. La solution est particulièrement adaptée au déploiement de VPN (virtual private networks, des réseaux sécurisés reliant les différentes entités physique d’une même organisation).
Crypta Labs (2013, UK, $300K) développe des solutions de chiffrement post-quantiques adaptées aux objets connectés. Ils proposent notamment le seul générateur de nombres aléatoire quantique intégrable dans un mobile. Ils travaillent de concert avec l’Université de Bristol.
evolutionQ (2015, Canada) est une startup qui se distingue surtout par le pédigrée de son créateur, Michele Mosca, un spécialiste Italien de la cryptographie post-quantique. C’est aussi le fondateur de l’Institut for Quantum Computing de l’Université de Waterloo au Canada. La société fait ce que l’on appelle du service outillé pour accompagner les entreprises dans l’adoption de cryptographie post-quantique. Cela commence par un produit d’évaluation du risque quantique (“Quantum Risk Assessment”) qui comporte six phases, documentées dans A Methodology for Quantum Risk Assessment, publié en 2017. Est-ce vraiment un produit ? Cela ressemble surtout à une méthodologie à mettre en œuvre avec des consultants. Le reste est de la même crème avec des services d’intégration et de formation pour faire évoluer les systèmes de cryptographie de l’entreprise.
ID Quantique (2001, Suisse, $5,6M) est l’une des plus anciennes sociétés du secteur, créée par le chercheur Suisse Nicolas Gisin, spécialiste de la photonique et de l’intrication quantique. La société propose surtout Quantis, son générateur de nombres aléatoires, déjà décrit au début de cette partie. C’est complété par Cerberis, une solution de QKD pour protéger la circulation des clés de chiffrement et Centauris, une gamme de serveurs de chiffrement supportant des liaisons optiques de 100 GBits/s. Ce serveur à base de FPGA supporte pour l’instant des systèmes à base de courbes elliptiques ainsi que de l’AES-256, dans l’attente de la standardisation des protocoles de PQC (post-quantum-crypto).
La startup appartient depuis début 2018 au groupe coréen SKT Invest qui est la branche de Corporate Venture de SK Telecom. Le fonds a investi $65M dans la startup dans ce qui est pudiquement présenté comme un partenariat alors que c’est une prise de contrôle. La société avait 60 salariés en juin 2018.
InfiniQuant (Allemagne) est une spin-off du Max Planck Institute for the Science of Light. Ils mettent au point un système de clé quantique QKD dénommé CV-QKD pour “Continuous Variable Quantum Key Distribution” utilisable sur fibre optique et liaison satellite. Cette technique utilise une modulation d’amplitude en plus d’une modulation de phase pour transmettre les clés quantiques. La startup travaille aussi sur un générateur de nombres aléatoire quantique, concurrent de ceux d’IDQ.
ISARA (2015, Canada, $1,6M de CA en 2017) développe des solutions logicielles de chiffrement post-quantiques et du conseil de mise en œuvre de PQC. Leur produit est la “ISARA Radiate Security Solution Suite” qui fournit des clés publiques et algorithmes de chiffrement non attaquables par des ordinateurs quantiques du futur. Ils s’appuient visiblement sur des arbres de hashage et associent de la PQC (post-quantum crypto) et de la PKI (public-key infrastructure) traditionnelle. C’est documenté dans le livre blanc Enabling Quantum-Safe Migration with Crypto-Agile Certificates, 2018 (7 pages). L’un de leurs investisseurs est le fonds Quantum Valley Investments, géré notamment par Mike Lazaridis, le cofondateur de Blackberry RIM. Ce dernier est une sorte de Xavier Niel canadien, ayant réinvesti sa fortune liée à Blackberry dans le développement de l’écosystème scientifique et entrepreneurial canadien, en particulier dans le quantique où il a investit en tout $450M (source).
KETS Quantum Security (2016, UK) développe un générateur de nombres aléatoire (QRNG = quantum random number generator) et un générateur de clé quantique QKD, le tout sur la base d’une photonique miniaturisée dans un simple composant. Le tout est combiné à une activité de conseil pour le déploiement des solutions. La société a été créée par des chercheurs en photonique de l’Université de Bristol. Ils ciblent les marchés financiers et du secteur public.
Magiq (1999, USA) est une startup qui s’était lancé initialement en 2003 dans la création d’un système de QKD. Depuis une dizaine d’année, cette société semble s’être repositionnée dans le service et pour la défense US. Ils ont développé l’Agile Interference Mitigation System (AIMS), un système de réduction d’interférences de communications électromagnétiques.
PicoQuant (1996, Allemagne) est une PME de Berlin spécialisée en photonique et qui commercialise notamment des compteurs de photons. Mais ils sont ici parce qu’ils proposent aussi un générateur de nombres aléatoire quantique.
Post Quantum (2009, UK, $10,4M) est une startup initialement créée sous l’appellation SRD Wireless qui avait créé la messagerie sécurisée PQ Chat utilisant les codes linéaires aléatoires inventés par Robert McEliece. La société a été renommée en Post-Quantum ou PQ Solutions Limited en 2014. Ils proposent une ligne de produits de sécurisation intégrant des algorithmes de crypto post-quantique. L’un des cofondateurs Martin Tomlinson, a développé le préencodage Tomlinson-Harashima qui permet de corriger les interférences dans les signaux de télécommunications et divers codes de correction d’erreur. Leurs produits comprennent aussi notamment PQ Guard, un système de chiffrement post-quantique.
QuantumCTek (Chine) est un fournisseur de solution de cryptographie quantique de bout en bout : QKD, répéteurs de QKD, routeurs optiques. La société est issue du Hefei National Laboratory for Physical Science at Micro-scale (HFNL) et de l’University of Science and Technology of China (USTC). Ils sont à l’origine de la création en 2014 du “Quantum-Safe Security Working Group” avec ID Quantique et Battelle, qui fait la promotion de la PQC. Ils ont comme nous l’avons vu plus haut déployé la liaison protégée par QKD de 2000 km reliant Shanghaï et Beijing.
Qasky (2016, Chine) commercialise le produit de la recherche de l’académie chinoise des sciences. Les financements proviennent de Wuhu Construction and Investment Ltd et de l’Université des Sciences et de Technologie de Chine. Ils proposent des solutions de crypto post-quantique, QKD et des composants de photonique. Leur nom est dérivé de CAS Key laboratory, CAS = Chine Academy of Sciences.
Qrypt (2017, USA) est une jeune startup de faisant de la PQC (post quantum crypto) créée par des anciens du gouvernement fédéral US, sans plus de précisions. Ils annonçaient en août 2018 utiliser sous licence le générateur de nombres aléatoire quantique à photons du laboratoire d’Oak Ridge du Département de l’Energie US.
Quintessence Labs (2006, Australie) propose un générateur de nombres aléatoires quantiques et un système de QKD. Ils utilisent la technique CV-QKD qui permet d’utiliser des infrastructures de fibre optique existantes des opérateurs télécoms à très haut débit.
Qunnect (2017, USA) est une toute jeune spin-off de la Stony Brook University de Long Island. Ils proposent des composants qui permettent d’upgrader des installations télécom existantes avec de la QKD et de la PQC, dont des sources de photons et une mémoire quantique fonctionnant à température ambiante pouvant servir à la mise en place de répéteurs de QKD (ci-dessous).
QuNu Labs (2016, Inde) développe des solutions à base de QKD issues de L’Institut de Technologie de Madras. Ils proposent aussi leur propre générateur de nombres aléatoires quantique et planchent aussi sur la création d’une solution de QKD opérant sur du Li-Fi, le W-FI qui utilise les fréquences de la lumière visible.
Secure-IC (France) est le porteur du projet RISQ, de création d’une solution de crypto post-quantique française. La société développe des solutions matérielles et logicielles de sécurité qui servent à évaluer la robustesse de solutions de sécurité. La société est issue de l’Institut Mines-Télécom.
SeQureNet (2008-2017, France) est une spin-off de Telecom ParisTech spécialisée dans la distribution de CV-QKD fonctionnant à longue distance (source). Elle a été financée dans le cadre du projet de recherche Européen SECOQC (secure communication based on quantum cryptography). Elle valorise des travaux issus de l’équipe de Philippe Grangier de l’Institut d’Optique et du laboratoire du CNRS situé chez Thales TRT à Palaiseau. Selon societe.com, la société a fermé boutique en 2017 ! Dommage.
S-Fifteen Space Systems (Singapour) est spécialisée dans la distribution de QKD par satellite. Ils valorisent des travaux de l’Université de Singapour dans la conception de pico-satellites de type CubeSat, pour la distribution de clés QKD.
Hors startups, des offres commerciales de cryptographie quantique et post-quantique sont aussi proposées ou sur le point d’être proposées par divers acteurs industriels tels que Batelle, Infineon, Raytheon, IBM, Cisco, Atos, Gemalto, Microsoft, NEC, Toshiba, Huawei, KT et Samsung.
Voilà pour cette petite liste. Il en manque sûrement et je les ajouterai au fil de l’eau si nécessaire, lorsque les lecteurs me le signaleront ou que j’en ferai la découverte.
____________________________________
Ouf. C’était finalement l’article le plus long de cette série !
Dans le prochain épisode, je ferais un tour d’horizon des stratégies quantiques pays par pays (USA, Chine, Japon, Europe, France, UK, Suisse, …).
Dans celui d’après, nous allons faire une arabesque latérale et couvrir un champ curieux, celui de la médecine quantique. Il a démarré avant la vague de l’informatique quantique et fait partie des domaines où se mélangent des travaux de recherche pertinents à bas niveau en biologie quantique et de fausses sciences pour gogos à haut niveau. C’est en quelque sorte du quantique-washing !
![]()
![]()
![]()
Reçevez par email les alertes de parution de nouveaux articles :
![]()
![]()
![]()
























































 Articles
Articles
Super complet : “Comprendre l’informatique quantique – cryptographie” de @olivez sur https://t.co/bWhzlp5HKy
Comprendre l’informatique quantique – cryptographie (là, c’est vraiment dodu) https://t.co/jhUmIx5yxn
Bonjour,
gros et beau travail comme toujours !
sinon pour AgilePQ il devrait changer de nom pour le développement en France 😉
En effet ! Mais avec les Qubits on est aussi bien servis… 🙂 ! On n’est donc plus à cela près !
Cet article est incroyable…. “Comprendre l’informatique quantique – cryptographie” de @olivez sur https://t.co/5w6ChqXO5g
@PierreMetivier @CNRS L’article de @olivez sur #QKD peut vous éclairer sur le sujet. Il y a des contres mesures qua… https://t.co/DkgztUpkXq
@fannysparty @Korben Indeed. Tous les détails ici, surtout sur la PQC (Post-Quantum Cryptography) : https://t.co/FTkZQx0GHe