Après avoir décrit les principes de base de la physique quantique puis ceux des qubits dans cette longue série sur l’informatique quantique, nous allons aller plus loin et décrire le fonctionnement opérationnel et physique d’un ordinateur quantique.
Il ne suffit en effet pas de répéter à l’envie que les qubits sont capables d’avoir à la fois la valeur 0 et 1. Il reste à comprendre comment ils sont mis en œuvre d’un point de vue pratique ! La compréhension de cette mise en œuvre est ensuite à relier aux algorithmes quantiques. Qui plus est, les architectures d’ordinateurs quantiques dépendent étroitement des caractéristiques de leurs qubits et les algorithmes utilisés ne sont pas forcément les mêmes selon ces architectures !
Certains comme le Français Atos ont cependant créé des outils de programmation quantiques qui se veulent indépendants des architectures matérielles. Un peu comme un compilateur C ou C++ qui peut générer du code binaire exécutable sur des processeurs différents. Cela peut fonctionner s’il existe une équivalence théorique entre les différents modèles d’ordinateurs quantiques. Il se trouve que c’est à peu près le cas donc tout va bien.
Pour être précis, dans ce qui suit, nous allons nous appuyer sur l’architecture d’ordinateurs quantiques universels à portes quantiques qui est la plus courante, celle des qubits à base de supraconducteurs à effet Josephson. Elle est notamment utilisée par IBM, Google, Intel et la startup américaine Rigetti. Une bonne part des éléments évoqués ici sont cependant applicables aux calculateurs quantiques utilisant d’autres types de qubits.
Poupées russes de l’ordinateur quantique
Nous allons démarrer ici par une vue d’ensemble de l’architecture générale d’un ordinateur quantique.
Tout d’abord, un peu comme pour les GPU, les ordinateurs quantiques sont mis en œuvre comme des coprocesseurs d’ordinateurs traditionnels qui les alimentent. Un ordinateur quantique est toujours un coprocesseur d’un ordinateur traditionnel, comme peut l’être un GPU pour les jeux vidéos ou pour l’entrainement de réseaux de neurones dans le deep learning.
Ces ordinateurs classiques servent à exécuter les programmes destinés au processeur quantique pour les traduire en opérations physiques à réaliser sur les qubits et à en interpréter les résultats. Des données sont utilisées pour initialiser l’état des qubits. L’ordinateur traditionnel pilote de près le fonctionnement de l’ordinateur quantique en déclenchant à un rythme précis les opérations sur les qubits qui sont réalisées par les portes quantiques. Ce déclenchement tient compte du temps d’exécution des portes quantiques et du temps de cohérence connu des qubits, c’est-à-dire, le temps pendant lequel les qubits restent en état de superposition.
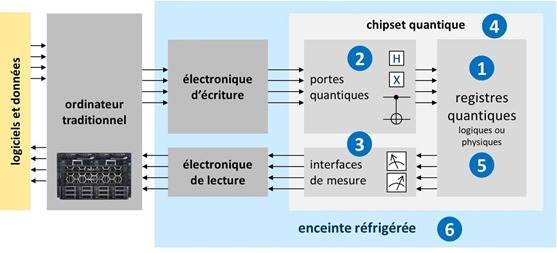
En plus de son ordinateur classique de contrôle, notre ordinateur quantique comprend au minimum les composantes labellisées de 1 à 6 que nous allons décortiquer une par une, d’abord avec une vue d’ensemble ci-dessous, puis avec une vue plus détaillée juste après.
(1) Les registres quantiques sont des collections de qubits. En 2018, ils n’en comprennent qu’à peine quelques dizaines. Ce sont eux qui stockent l’information manipulée dans l’ordinateur et exploitent le principe de superposition permettant de faire cohabiter un grand nombre de valeurs dans ces registres et d’opérer des opérations dessus simultanément.
(2) Les portes quantiques sont des dispositifs physiques agissant sur les qubits des registres quantiques, à la fois pour les initialiser et pour y effectuer des opérations de calcul. Ces portes sont appliquées de manière itérative, au gré des algorithmes à exécuter. L’électronique de commande des qubits pilote les dispositifs physiques qui servent à initialiser, modifier et lire l’état des qubits. Dans les qubits supraconducteurs, les portes quantiques sont activées avec des générateurs de micro-ondes de fréquences comprises entre 5 et 10 Ghz. Ces micro-ondes circulent sur des fils électriques conducteurs entre leur source et le processeur quantique. Leurs générateurs prennent encore de la place. Ils ne sont pas très miniaturisés à ce stade, générant un facteur limitant du nombre de qubits qui sont intégrables dans un calculateur quantique.
(3) Des dispositifs physiques de mesure de l’état des qubits permettent d’obtenir le résultat des calculs à la fin du processus d’exécution séquentielle des portes quantiques. Dans certains types d’ordinateurs quantiques comme les systèmes à recuit quantique de D-Wave, on peut appliquer ce cycle d’initialisation, de calculs et de mesure plusieurs fois pour évaluer plusieurs fois le résultat. On obtient alors par moyenne une valeur comprise entre 0 et 1 pour chaque qubit des registres de l’ordinateur quantique. Les valeurs lues par les dispositifs physiques de lecture sont ensuite converties en valeurs numériques et transmises à l’ordinateur classique qui pilote l’ensemble et permet l’interprétation des résultats. Les dispositifs de lecture sont reliés à leur électronique de contrôle via des fils supraconducteurs dans le cas des qubits d’ordinateurs supraconducteurs.
(4) Le chipset quantique comprend les registres quantiques, les portes quantiques et les dispositifs de mesure lorsqu’il s’agit de qubits à supraconducteurs ou à quantum dots. Les dispositifs sont plus hétérogènes pour les autres types de qubits, notamment ceux qui exploitent des lasers et des photons pour l’initialisation, les portes quantiques et la mesure des qubits. Les chipsets actuels ne sont pas très grands. Ils font la taille d’un capteur photo full-frame ou double-format pour les plus grands d’entre eux. Chaque qubit est relativement grand, leur taille se mesurant en microns alors que les transistors de processeurs modernes en CMOS ont des tailles maintenant inférieures à 20 nanomètres.
(5) Les qubits logiques regroupent des qubits physiques pour permettre une mise en œuvre de correction d’erreurs à l’échelle physique de l’ordinateur. D’autres méthodes utilisent des corrections d’erreurs au niveau algorithmique par l’utilisation de codes de correction d’erreurs à base de portes quantiques. La gestion des erreurs engendrées par les opérations effectuées sur les qubits est un des plus gros casse-tête de la mise au point d’ordinateurs quantiques.
(6) Une enceinte cryogénisée maintient l’intérieur de l’ordinateur à une température voisine du zéro absolu. Elle contient une partie de l’électronique de commande et le ou les chipsets quantiques pour éviter de générer des perturbations empêchant les qubits de fonctionner, notamment au niveau de leur intrication et cohérence ainsi que pour réduire le bruit de leur fonctionnement. Le Graal serait de pouvoir faire fonctionner des qubits à température ambiante mais les architectures correspondantes comme dans les NV Vacancy ou cavités de diamants ne sont pas encore opérationnelles.
Pour réaliser le schéma ci-dessus qui explique tout cela, je me suis inspiré du slide 14 de la présentation Quantum Computing (and Quantum Information Science) de Steve Binkley, US Department of Energy, 2016 (23 slides).
Voyons donc tout cela en détail !
Registres
Dans un ordinateur quantique, les qubits sont organisés par blocs qui constituent des registres. Un peu comme les registres 32 ou 64 bits des processeurs classiques actuels. L’histoire ne dit pas encore si les ordinateurs de plusieurs millions de qubits utiliseront des registres de cette taille ou des registres de taille raisonnable. Les architectures envisagées sont diverses, comme celles qui utiliseraient des registres de qubits qui seraient ensuite reliés entre eux de diverses manières, via des portes quantiques et/ou de l’intrication.
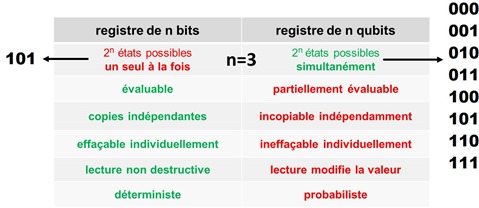
La principale différence entre un registre de n qubits et un registre traditionnel de n bits est la quantité d’information qui peut y être manipulée simultanément. Dans les ordinateurs classiques, ce sont par exemple des registres de 32 ou 64 bits qui stockent des entiers ou des nombres flottants sur lesquels sont réalisées des opérations mathématiques élémentaires.
Les qubits présentent l’avantage de pouvoir osciller en permanence entre la valeur 0 et 1, selon le principe de la superposition des états quantiques. L’oscillation est une vue de l’esprit qui ne correspond pas forcément à la réalité physique mais permet de se faire une idée conceptuelle de cette notion de superposition.
Un registre de n qubits peut donc avoir toutes les valeurs possibles à un moment donné. Pour prendre l’exemple d’un registre de 3 bits et de 3 qubits, le premier stockera une seule valeur à la fois comme 101 (5 en base 2) tandis que le registre de trois qubits va faire cohabiter par superposition toutes les valeurs possibles de ce registre, qui sont au nombre de 2 puissance 3, soient 8. C’est ce qui permet de faire des calculs à combinatoire exponentielle.
Ces “2 puissance n” d’états ne correspondent toutefois pas véritablement à une capacité de stockage d’information. C’est une capacité de superposition d’états auxquels on applique ensuite des traitements pour faire ressortir les combinaisons que l’on recherche selon un algorithme donné. Cela permet de tester plein d’hypothèses en parallèle pour faire ressortir la meilleure. L’information pertinente est ce résultat qui se manifeste après lecture sous la forme d’un registre classique de bits. La combinatoire de toutes les valeurs de registres pendant les calculs n’est pas une information utile en soi. C’est l’information qui en est extraite qui a de la valeur.
Ne croyez donc pas ceux qui vous font miroiter des applications de type “big data” grâce à la combinatoire des états des qubits. Comme cette combinatoire n’intervient que pendant les calculs et ni en entrée ni en sortie, il faut raison garder !
Les états superposés des registres vérifient une loi de distribution probabiliste selon laquelle le total de la probabilité de chaque état superposé est égal à 1 comme indiqué dans le schéma ci-dessous. Un calcul quantique va faire évoluer dans le temps la probabilité de chacune des combinaisons d’états de qubits (|x> dans la formule ci-dessous). L’idée est de faire converger après plusieurs opérations la valeur du registre quantique vers la valeur recherchée que l’on lit ensuite de manière classique pour obtenir une suite de n 0 et 1 contenant la réponse. Comme par exemple un nombre premier diviseur d’un nombre entier fourni en entrée.
Ce schéma est inspiré de Modèles de Calcul Quantique (30 pages), de Pablo Arrighi et Simon Perdrix, un document très bien fait qui explique avec quelques formules mathématiques pas trop compliquées comment fonctionne le calcul quantique. Il explique notamment très bien l’algorithme de Deutsch-Jozsa sur lequel je reviendrai dans la partie suivante de cette série.
Ceci est renforcé par le fait que lorsqu’on lit le contenu d’un qubit, on récupère 0 ou 1 et donc une seule combinaison des 0 et 1 des qubits du registre. En le faisant plusieurs fois de suite après avoir exécuté l’ensemble de l’algorithme, on récupère un % de 0 et un % de 1. Idem pour tous les qubits d’un registre. On ne récupère donc pas 2 puissance n valeurs dans la pratique, on récupère n nombres flottants avec une précision dépendante de la précision de la mesure de l’état des qubits et du bruit qu’ils subissent de l’environnement et qui perturbe leur état de superposition. Mais cela dépend des algorithmes. Pour la majorité d’entre eux, une information binaire en sortie est suffisante comme pour l’algorithme de factorisation de nombres entiers de Peter Shor. Mon histoire de % entre 0 et 1 est une possibilité théorique. Je ne l’ai rencontrée que dans le cas de certains algorithmes pour ordinateurs de D-Wave qui reposent sur un fonctionnement particulier et que nous décrirons dans une autre partie.
On est sinon contraint par le théorème de Holevo de 1973 qui prouve qu’avec n qubit on ne peut pas récupérer plus que n bits d’information après un calcul quantique (source) !
Au stade actuel de mise au point des qubits, leur taux d’erreur est situé aux environs de 0,5% environ et il faudrait idéalement qu’il soit de 0,01% voire 0,0001%. Ce taux d’erreur s’évalue d’ailleurs au niveau de la stabilité de chaque qubit pris isolément et des opérations de portes quantiques portant sur deux qubits. La superposition des valeurs dans les registres quantiques est préservée pendant les opérations de portes quantiques qui présentent la particularité de ne pas faire sortir les qubits de leur état de superposition. Seule la mesure le fait. C’est la magie des algorithmes quantiques que de l’exploiter pour faire ressortir à la fin le résultat recherché. Vous suivez ?
Cela ne présente donc pas grand intérêt de comparer l’énorme combinatoire des registres qubits avec le nombre de particules dans l’Univers comme certains le font souvent. Ce ne sont pas des données équivalentes. Une combinatoire d’états n’est pas homothétique avec un nombre d’objets. Avec un nombre d’objets donné, la combinatoire de ces objets représentera toujours un nombre largement supérieur au nombre d’objets pris en référence. Imaginez donc la combinatoire pour positionner dans l’espace toutes les particules de l’Univers !
Par contre, sorti de cette combinatoire, les qubits ont plein d’inconvénients en opposition totale avec les bits classiques. On ne peut ni copier classiquement ni effacer individuellement la valeur des qubits lorsqu’ils sont ensuite intriqués entre eux. Leur mesure les modifie. Ce sont des objets probabilistes délicats à manipuler. Par contre, sans en connaître la valeur interne (le fameux vecteur représenté par la sphère de Bloch vue dans la partie précédente), on peut agir dessus avec des portes quantiques, que l’on va voir juste après.
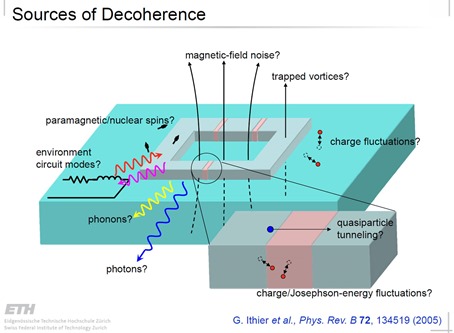
Un qubit est cohérent lorsqu’il est bien en état de superposition entre les deux niveaux possibles du qubit physique. Le temps de cohérence est une indication de la durée pendant laquelle les qubits d’un registre restent cohérents, donc en état de superposition. Pour être précis, le temps de cohérence est celui au bout duquel les qubits perdent leur cohérence.
Lorsque l’on effectue une mesure de l’état d’un qubit, on provoque sa décohérence puisque la mesure amène le qubit dans l’un de ses deux états de base possibles, en supprimant la superposition. D’autres événements physiques peuvent provoquer cette fin de superposition, ou décohérence. Ils proviennent du “bruit”, des chocs entre atomes et autres perturbations physiques. En voici un petit inventaire pour ce qui est des qubits supraconducteurs issus de la présentation Sources of decohence, de l’ETH Zurich, 2005 (23 slides). On y voit notamment évoqué le bruit magnétique, ce qui explique pourquoi D-Wave isole ses enceintes d’ordinateur quantique avec 16 couches métalliques pour limiter l’impact du magnétisme terrestre sur ses qubits.
On évite une partie de ces effets en refroidissant les qubits à une température proche du zéro absolu, mais ce n’est pas suffisant. Les chercheurs travaillent donc d’arrache-pied pour faire en sorte que le temps de cohérence des qubits soit le plus long possible et le bruit qui affecte les qubits le plus faible possible.
C’est une situation paradoxale : les qubits restent cohérents, donc en état de superposition, si on ne les dérange pas, mais on passe son temps à les déranger avec les opérations des portes quantiques qui agissent dessus ! En termes physiques, on veut donc en obtenir le beurre et l’argent du beurre !
Portes
Dans l’informatique classique, les portes logiques exécutent de l’algèbre booléenne avec des tables de décision en fonction des bits en entrée. Il y a plusieurs types de portes logiques à une et deux entrées, dont la porte NAND qui est intéressante car elle est universelle et n’utilise que deux transistors. On peut théoriquement créer les autres portes booléennes avec des portes NAND.
En général, les portes logiques sont cependant panachées dans les circuits. Un processeur Intel Core i5/7 avec de 5 milliards de transistors va comprendre au moins 1 à 2 milliards de portes logiques. Un processeur est évidemment très complexe avec des portes qui gèrent l’accès à une mémoire cache et aux registres et la lecture de programmes qui définissent les portes à utiliser dans les calculs. A partir de là, on peut presque tout faire ! Ces opérations sont générées à la fréquence d’horloge du processeur, exprimée en MHz ou, le plus souvent, en GHz.
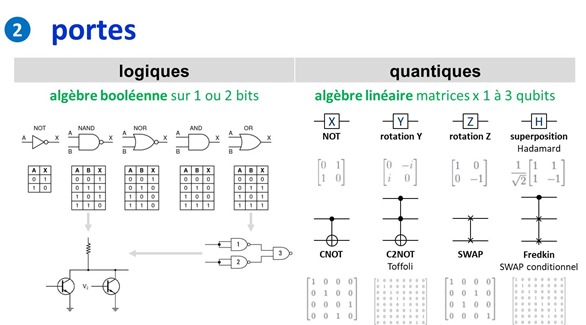
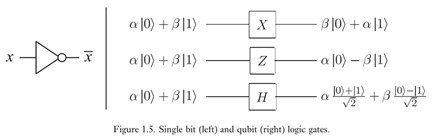
Les qubits qui stockent chacun un vecteur à deux dimensions subissent de leur côté des opérations via des portes quantiques qui leur appliquent des opérations d’algèbre linéaire sous forme de matrices 2×2 de nombres réels et complexes comme représentées ci-dessus.
Les portes quantiques modifient l’information des qubits sans les lire. Elles permettent aussi à l’information de circuler entre les qubits. Elles ne sont pas destructrices de l’état des qubits ou de leur cohérence contrairement aux systèmes de mesure qui interviennent en fin de calcul.
Comme pour la logique booléenne, il existe des portes unitaires agissant sur un seul qubit et des portes agissant sur plusieurs qubits de manière conditionnelle.
Dans les portes unitaires, les vecteurs à deux dimensions représentant l’état des qubits sont multipliés par des matrices unitaires. L’opération provoque une rotation du vecteur représentant la valeur du qubit en état de superposition dans la sphère de Bloch qui le représente géométriquement.
Les principales portes unitaires sont :
- La porte X ou NOT qui réalise une inversion. Un 0 devient un 1 et réciproquement. Mathématiquement, elle intervertit le alpha et le beta du vecteur à deux composantes qui représente l’état du qubit. Cette porte est souvent utilisée pour initialiser à 1 l’état d’un qubit en début de processus qui est par défaut à 1.
- La porte Y qui réalise une rotation d’un demi tour autour de l’axe Y dans la sphère de Bloch.
- La porte Z qui est un changement de signe appliqué sur la composante beta du vecteur du qubit. Les portes X, Y et Z sont dites “portes de Pauli”.
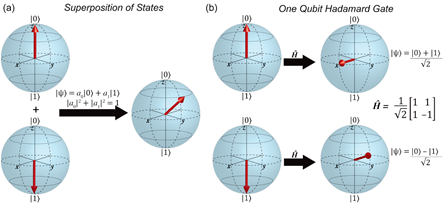
- La porte Hadamard-Walsh qui met un qubit à 0 ou 1 dans un état superposé “0 et 1”. Elle est fondamentale pour générer cette superposition d’états dans les registres que nous avons décrite dans la partie sur les registres. La porte de Hadamard est très souvent utilisée pour initialiser un registre quantique afin de générer cette combinatoire de “2 puissance n” valeurs différentes cohabitant simultanément dans un registre de n qubits. Par contre, les portes quantiques qui vont intriquer entre eux des qubits vont réduire cette combinatoire car les qubits intriqués vont être en quelque sorte synchronisés, et réduire la combinatoire de superposition d’états du registre quantique. Voici une représentation de l’effet de cette porte sur un qubit initialisé à 0 ou 1 dans la sphère de Bloch. Notons que si l’on applique deux fois de suite une porte de Hadamard à un qubit, on revient au point de départ.
Nous avons ensuite des portes à deux ou trois qubits comme :
- La porte CNOT qui est une inversion de la valeur d’un qubit conditionnée par la valeur 1 d’un autre qubit.
- La porte C2NOT ou de Toffoli est une inversion de la valeur d’un qubit conditionnée par la valeur 1 de deux autres qubits.
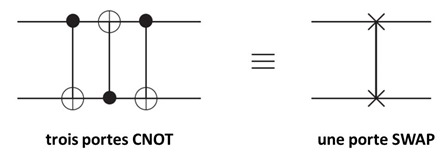
- La porte SWAP intervertit les valeurs quantiques de deux qubits. Elle peut d’ailleurs être générée à partir de l’enchaînement de trois portes CNOT consécutives (schéma ci-dessous).
- La porte de Fredkin est une porte SWAP conditionnée par l’état d’un troisième qubit. Elle a donc trois entrées.
- La porte S qui permet un changement de phase d’un qubit contrôlé par l’état d’un qubit.
Ces portes à 2 ou 3 qubits y appliquent donc des transformations matricielles de respectivement 4×4 ou 8×8 entrées aux qubits en entrée. Soit 1 qubit = 2 nombres, 2 qubits = 4 nombres, 3 qubits = 8 nombres, la taille des matrices de transformation de l’état des qubits étant de 2 puissance le nombre de qubits transformés. Pourquoi donc ? Parce que ces matrices s’appliquent à chacun des états superposés possibles de la combinaison des qubits, et ce nombre d’états est 2 puissance N qubits.
Les portes de Toffoli et Fredkin sont dites complètes, car elles sont capables d’engendrer toutes les portes logiques de la combinatoire des circuits.
Un jeu de portes est dit universel lorsqu’il permet de recréer par assemblage temporel toutes les portes requises par les algorithmes courants. Plusieurs combinaisons de portes universelles sont possibles comme une porte CNOT et une SWAP, ou bien une porte de Hadamard complétée d’une porte CNOT. Une seule porte Toffoli est universelle. Selon Artur Ekert, presque toutes les portes à deux qubits sont universelles. La combinaison de portes universelles mises en œuvre physiquement dans les ordinateurs quantiques dépend de leur type et des dispositifs physiques qui agissent sur les qubits.
Les ordinateurs quantiques utilisent aussi des “ancillae qubits” ou qubits de contrôle de valeurs déterminée (0 en général) pouvant être combinées avec des qubits indéterminés (ceux du calcul). Ils sont aussi utilisés pour la correction quantique d’erreurs (QEC) expliquée plus loin. On n’en lit pas la valeur à la fin des traitements. C’est une sorte de poubelle de qubits utilisés pendant les calculs !
Les portes quantiques ont la particularité d’être théoriquement réversibles. On peut revenir en arrière si bon nous chante et sans perdre d’information en appliquant dans l’ordre inverse les portes quantiques qui viennent d’être appliquées à un registre de qubits. L’intérêt de la réversibilité est que les portes quantiques ne consomment pas ou peu d’énergie. C’est d’ailleurs une voie possible de réduction de consommation d’énergie pour les ordinateurs traditionnels, mais dont l’exploration est laborieuse. Il est en effet possible de créer des portes logiques traditionnelles réversibles ! Voir par exemple Generalized Reversible Computing and the Unconventional Computing Landscape de Michael Frank, 2017 (34 slides).
La notion de réversibilité d’un calcul quantique est théorique et ne sert donc pas à grand chose. On pourrait en théorie exécuter un algorithme quantique puis dérouler à l’envers cet algorithme et revenir au point de départ initial… avec des qubits initialisés à 0 ! Cela permettrait par exemple de partir d’un résultat connu et de revenir au point de départ, mais une suite de zéros n’est pas très intéressante ! Qui plus est, cela ne fonctionnerait pas bien parce que le bruit quantique perturberait l’opération et introduirait des erreurs. Cela ne servirait pas à grand chose et on ne pourrait pas mesurer l’état des qubits à la fin de l’exécution de l’algorithme avant l’exécution de l’algorithme inversé car cela rabattrait les vecteurs des qubits dans des valeurs basiques 0 et 1, qui rendraient caduque l’algorithme inverse.
Voici quelques sources d’information sur le sujet des portes quantiques qui ont éclairé ma lanterne : Universality of Quantum Gates de Markus Schmassmann, 2007 (22 slides), An introduction to Quantum Algorithms de Emma Strubell, 2011 (35 pages), L’ordinateur quantique, note de l’Ambassade de France à Washington de Daniel Ochoa, 2008 (70 pages), Equivalent Quantum Circuits de Juan Carlos Garcia-Escartin and Pedro Chamorro-Posada, 2011 (12 pages) et The Future of Computing Depends on Making It Reversible de Michael P. Frank, 2017.
Entrées et sorties
Les microprocesseurs traditionnels sont composés de portes logiques fixes, gravées dans le silicium, et de bits ‘mobiles’, se présentant comme des impulsions électriques qui se propagent dans le circuit à travers les différentes portes. Le tout à une certaine fréquence, qui se compte souvent en GHz, réglée par une horloge à quartz.
Dans un ordinateur quantique, la première étape des traitements consiste à mettre le système quantique représenté par son ou ses registres quantiques dans un état initial. On dit que l’on “prépare le système”. Les différents registres sont d’abord configurés physiquement dans l’état 0, chaque qubit étant à 0. L’initialisation qui suit consiste à faire agir différents opérateurs comme la transformation de Hadamard pour créer une superposition 0+1 ou la porte X pour modifier cette valeur 0 en 1.
Une fois cette initialisation réalisée sont lancées séquentiellement des opérations de portes sur les qubits en fonction de l’algorithme a exécuter. Enfin, on lit la valeur des qubits à la fin des traitements, ce qui a pour effet de modifier leur état quantique.
Physiquement, les qubits ne bougent pas. Les portes non plus. Les portes sont activées dynamiquement et opèrent sur les qubits. Les diagrammes de représentation des algorithmes quantiques (ci-dessous à droite) sont en fait des schémas temporels alors que pour les portes logiques classiques, il s’agit un diagramme physique.
J’ai mis beaucoup de temps à comprendre cela car une partie de la littérature technique sur les processeurs quantiques assimile les lignes horizontales de ces algorithmes à des “fils” reliant les qubits en entrée à des qubits en sortie, ce qui est entièrement faux. Dans la partie droite décrivant un algorithme quantique, il n’y a pas de fils physiques reliant les qbits entre une entrée et une sortie, les portes étant sur leur chemin. C’est un schéma temporel !

Layout physique
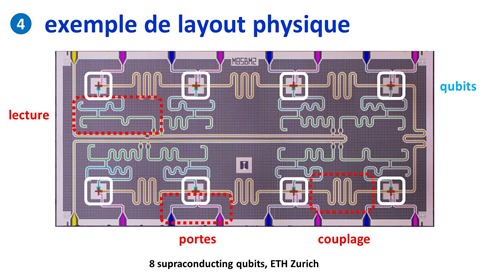
Pour mieux comprendre l’explication précédente, voici un layout de chipset de 8 qubits, issu de l’ETH Zurich qui date déjà de quelques années. Ce n’est qu’un exemple illustratif car les layouts physiques sont très variables d’un type de qubit à un autre. Mais le principe décrit ici est commun à tous les ordinateurs quantiques à base de supraconducteurs.
On y voit très bien que, dans le circuit :
- Les qubits sont situés dans les rectangles blancs. Ce sont eux qui intègrent une boucle à effet Josephson.
- Ils sont reliés entre eux par des circuits de couplage qui servent à contrôler leur intrication.
- Des portes bleue et violette permettent d’agir sur les qubits. Ces deux portes sont des portes universelles permettant par combinaison de recréer les autres portes quantiques nécessaires à l’exécution des algorithmes. Dans la pratique, avec les qubits supraconducteurs, ces “pins” sont alimentés via des câbles par des sources de courants à très haute fréquence, dites micro-ondes, comprises entre 5 et 10 GHz. Ces fréquences peuvent être différentes entre les différents qubits d’un même circuit.
- La mesure a lieu avec d’autres circuits, eux aussi fixes dans le composant. Dans les qubits supraconducteurs, ce sont des magnétomètres.
Dans un ordinateur quantique, on cherche à faire en sorte que les qubits interagissent entre eux mais le moins possible avec leur environnement jusqu’à ce que l’on mesure leur état ! C’est pour cela qu’ils sont généralement refroidis à une température proche du zéro absolu et isolés magnétiquement de l’extérieur. Le choix des matériaux des chipsets joue aussi un rôle pour minimiser le bruit qui pourrait affecter les qubits et les faire sortir de leur état de superposition.
Source de l’image : The European Quantum Technologies Roadmap 2017 (30 pages).
Et voici une autre représentation, originaire de Google, expliquant la même chose, vue dans : The Question of Quantum Supremacy, paru en mai 2018 et qui référence deux papiers sur la suprématie quantique recherchée par Google : Characterizing Quantum Supremacy in Near-Term Devices et A blueprint for demonstrating quantum supremacy with superconducting qubits.
Dans le schéma ci-dessous, voici le pourquoi du comment de la relation entre “gate time” (temps d’activation des portes) et le temps de cohérence pendant lequel les qubits restent en place et surtout, restent intriqués et en état de superposition. Et je vous passe les histoires de temps de “relaxation” après l’activation des portes.
Sachant que l’intrication ne concerne a priori qu’une partie des qubits des registres. Les ordres de grandeur de ces temps pour un ordinateur quantique classique, notamment supraconducteur, donnent au mieux un rapport de 1 à 500 entre temps de portes et durée de cohérence. Ce qui veut dire que l’on sera limité pour ce qui est du nombre de portes quantiques utilisables dans un algorithme, ce d’autant plus qu’une bonne part de ces portes sera utilisée pour les codes de correction d’erreurs. Dans les premières générations d’ordinateurs quantiques d’IBM, les portes X, d’Hadamard et CNOT duraient respectivement 130 ns, 130 ns et 650 ns.
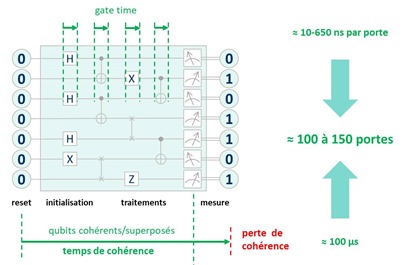
Ces indications fournissent une limite haute du nombre de portes qui peuvent être enchaînées dans un algorithme quantique. A noter que ces temps sont plus longs pour les ordinateurs quantiques à ions piégés mais les gate time y sont aussi plus longs. Dans les qubits CMOS, les temps de cohérence sont plus longs et les gate time sont faibles.
Dans les schémas décrivant des algorithmes quantiques, comme celui ci-dessus, la double barre après la mesure de l’état d’un qubit indique par convention que l’on a récupéré un bit normal, à 0 ou 1. Au passage, tout ceci rappelle qu’il y a autant de qubits en sortie qu’en entrée dans un calcul quantique puisque ce sont physiquement les mêmes !
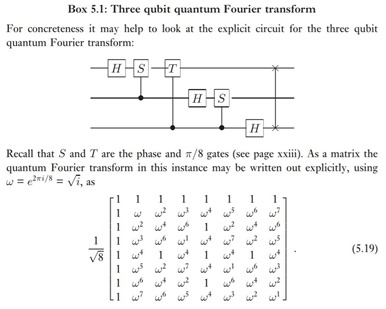
Mathématiquement parlant, une suite de porte quantiques dans un ordinateur quantique est représentable par une matrice de 2^N x 2^N nombres complexes, N étant le nombre de qubits utilisés. Elle peut être donc immense dès que N dépasse 10. Multipliée par le “tenseur” comprenant les N qubits en entrées (initialisés à 0), elle génère une combinaison de N qubits en sortie.
Le schéma ci-dessus (source) en est un exemple avec la matrice correspondant à un algorithme de transformée de Fourier quantique appliquée à un jeu de 3 qubits. 2 puissance 3 donne 8 qui correspond aux deux dimensions de la matrice de transformation de l’algorithme. Imaginez alors la taille de la matrice pour 2 puissance 1024 !
La taille de cette matrice devient gigantesque dès que N dépasse 50. Il se trouve qu’on utilise de telles matrices dans les simulateurs d’algorithmes quantiques à base de supercalculateurs classiques. Au-delà de 56 qubits, la taille de la matrice devient trop grande pour rentrer en RAM dans ces ordinateurs. Cela explique pourquoi les simulateurs d’ordinateurs quantiques sur supercalculateurs sont limités à environ une cinquantaine de qubits. Au-delà, la taille de la matrice à simuler est bien trop grande par rapport à la capacité mémoire de ces supercalculateurs. On n’est cependant peut-être pas obligé de simuler une matrice entière. Il est peut-être possible de simuler en mémoire l’état du registre des qubits avec un vecteur de N fois deux nombres complexes. En fait, je ne sais pas trop !
Correction d’erreurs
L’un des écueils des qubits est qu’ils génèrent un taux d’erreurs non négligeable pendant que l’on agit sur eux avec des portes quantiques.
Ces erreurs ne sont pas seulement des inversions simples de 0 et de 1 comme dans l’informatique traditionnelle, mais des glissements de valeurs des vecteurs représentant les qubits avec des modifications de phases lors de la superposition des qubits. Dans la sphère de Bloch, ce sont des vecteurs horizontaux qui peuvent tourner légèrement autour de l’axe vertical. Ces erreurs sont liées aux interactions entre les qubits et leur environnement, en plus du problème du temps de cohérence, qui est le temps pendant lequel les qubits restent en état de superposition.
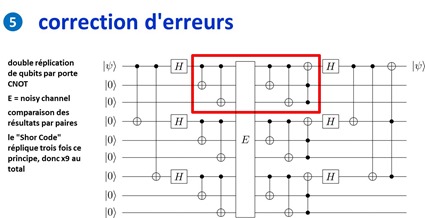
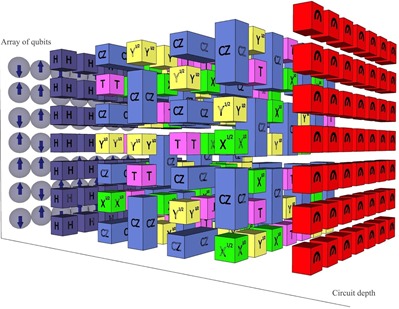
Avec les qubits actuels, le taux d’erreurs courant peut atteindre 0,1% à 1%, ce qui est bien supérieur aux taux d’erreurs courants de l’informatique traditionnelle. Il faut donc mettre en œuvre des systèmes de correction d’erreurs que l’on appelle QEC pour Quantum Error Correction. Ils conduisent à répliquer plusieurs fois par intrication les qubits de calcul pour leur faire subir le même traitement en parallèle et à comparer les résultats en sortie d’algorithme pour conserver les résultats statistiquement dominants. Le tout sans lire la valeur des qubits qui ferait effondrer tout le système !
L’un des algorithmes les plus couramment utilisé duplique un qubit deux fois (dans le cadre rouge de l’illustration ci-dessous). Après le passage par un processus de calcul générateur de bruit (E), la différence entre les trois versions est évaluée. S’il y a une différence, on retient les qubits inchangés majoritairement. Le code de Shor est une déclinaison par trois de cette méthode, ce qui conduit un qubit donné à être répliqué 8 fois en tout. L’intérêt de la méthode qui s’appuie sur des portes quantiques classiques CNOT est qu’il ne nécessite pas de lire – et donc de détruire – la valeur des qubits. C’est un code de correction d’erreurs non destructif ! Le détail du processus est bien documenté dans la fiche Wikipedia de la correction d’erreur quantique. Ce code de correction d’erreurs à 9 qubits permet de corriger à la fois les erreurs d’inversion (0 à la place de 1 et réciproquement) et les erreurs de phase (modification du de la composante verticale du qubits dans sa sphère de Bloch).
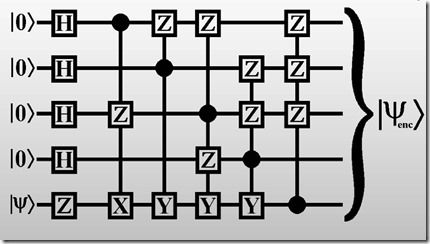
Il semblerait qu’il faille au moins cinq qubits “physiques” pour créer un qubit logique intégrant la correction d’erreurs. Cf l’algorithme ci-dessous, vu dans Magic States de Nathan Babcock (28 slides).
Dans la pratique, on va donc assembler des qubits physiques en qubits logiques avec de la redondance et des systèmes de correction d’erreurs au niveau des circuits et processeurs quantiques.
La notion de qubits logiques peut être mise en œuvre soit par logiciel, soit au niveau matériel. Lorsqu’elle est logicielle, c’est le rôle des algorithmes que de mettre en œuvre des codes de correction d’erreur dynamiques. Lorsque l’on utilise la vingtaine de qubits physiques en cloud proposée par IBM, c’est au développeur de mettre en œuvre ses propres codes de correction d’erreur.
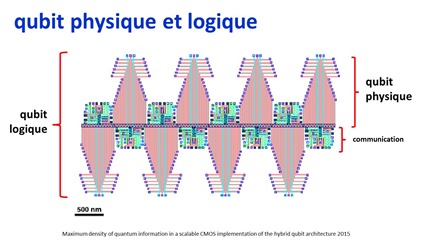
Dans une QEC (Quantum Error Correction) réalisée au niveau matériel, celle-ci est mise en œuvre par création d’assemblage de qubits qui génèreront des qubits logiques physiques prêts à l’emploi. En voici un exemple avec sept qubits physiques pour constituer un qubit logique. Il vient de Maximum density of quantum information in a scalable CMOS implementation of the hybrid qubit architecture, 2015 (17 pages). La raison d’être de cette architecture est liée au fait que les qubits en CMOS génèrent plus de bruit que les qubits en supraconducteurs à effet Josephson. On doit donc en passer par là pour réduire le bruit. Sachant… que cela ne fonctionne pas encore ! Et que l’usage de seulement huit qubits physiques pour créer un qubit logique est sujet à caution.
Le nombre de qubits physiques à assembler pour créer un qubit logique dépend du taux d’erreurs des qubits. Plus le taux d’erreurs des qubits est élevé, plus grand doit être le nombre de qubits assemblés. Ce nombre peut atteindre plusieurs milliers de qubits ! Pour Alain Aspect, il faudrait avoir un million de qubits physiques par qubit logique pour créer un ordinateur quantique utilisable. Ce qui veut dire que pour avoir ne serait-ce que quelques centaines de qubits logiques à même d’atteindre la suprématie quantique pour des algorithmes quantiques assez simples, il faudrait disposer de plusieurs dizaines de millions de qubits physiques. On en est encore bien loin !
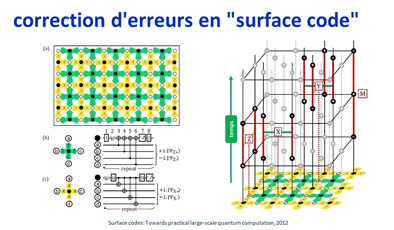
Dans le supraconducteur à effet Josephson, la technologie de correction d’erreurs la plus souvent envisagée s’appelle le “surface code”, datant de 2012, et vue dans Surface codes towards practical large-scale quantum computation, 2012 (54 pages). Elle comprend des matrices de qubits reliés entre eux via des portes unitaires X et Z. Leur programmation dans le temps permet de corriger des erreurs. Mais elle ajoute une série de portes quantiques qui allongent la durée des opérations. Nous avons ici des portes de Pauli X (inversion), Pauli Z (changement de phase) reliées aux qubits. On peut voir à droite une timeline verticale ascendante de l’évolution de la valeur des qubits au gré de l’activation des portes pour la correction d’erreurs.
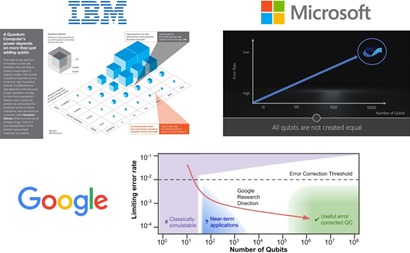
Tout ceci explique pourquoi IBM communique sur le couple nombre de qubits et le taux d’erreurs. Microsoft et Google font de même. Microsoft est d’ailleurs celui qui simplifie le plus la présentation. Une fois n’est pas coutume ! Bref, pour qu’un ordinateur quantique serve à quelque chose, il faut à la fois avoir beaucoup de qubits et un faible taux d’erreurs. Sources : IBM Bolsters Quantum Capability, Emphasizes Device Differentiation, 2017, et pour Microsoft, un extrait de la vidéo Future Decoded Quantum Computing Keynote, novembre 2017. Par contre, au-delà de ces slides, ces acteurs ne sont pas très bavards sur les taux d’erreurs effectifs de leurs qubits.
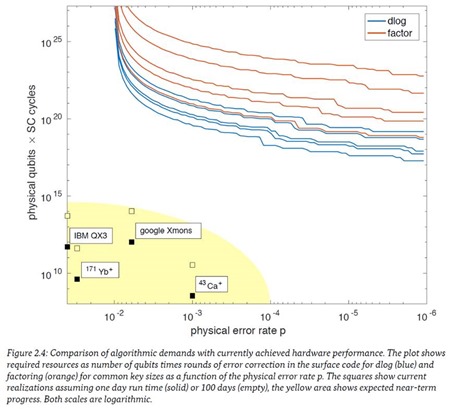
Il faut fouiller ailleurs pour en savoir plus, comme dans l’excellent rapport Entwicklungsstand Quantencomputer (état des lieux de l’informatique quantique) de l’ANSSI allemande qui met en évidence l’énorme décalage entre les performances actuelles des qubits, notamment chez IBM et Google, et le besoin lié à la factorisation de nombres entiers pour casser des clés RSA courantes. Même si ce besoin référent n’est pas le plus “constructif” parmi les domaines d’applications des ordinateurs quantiques.
Il semblerait cependant que cette notion de taux d’erreurs puisse être “scalable”. A savoir que lorsque l’on saura baisser le taux d’erreurs des qubits à un niveau acceptable, on pourra facilement démultiplier le nombre de qubits dans les circuits et conserver ce taux d’erreurs. Tout ça pour dire que l’abaissement du taux d’erreur des qubits est indépendant de leur nombre dans un circuit. Ce qui sous-tend, une fois ce problème de taux d’erreur réglé, que la montée en puissance des calculateurs quantiques en nombre de qubits pourrait être ensuite très rapide. C’est en tout cas ce que m’a raconté un chercheur d’IBM rencontré sur Vivatech en mai 2018. D’autres publications ne sont pas aussi radicales sur ce point et évoquent de nombreux obstacles pour faire “scaler” le nombre de qubits en préservant leur fiabilité.
Cryogénie
Pour terminer le tour de l’architecture d’un ordinateur quantique type, passons à la partie cryogénie. Lorsque l’on observe de près un ordinateur quantique issu des grands acteurs du secteur, on y décèle un petit air de famille comme ci-dessous avec les cas d’IBM, de Rigetti et de D-Wave. Ils présentent la particularité d’utiliser tous les trois des qubits à base de supraconducteurs. Cette technologie nécessite de refroidir les qubits à une température aussi basse que possible pour éviter toutes les perturbations du monde extérieur. L’isolation de l’ensemble doit être la plus totale possible.
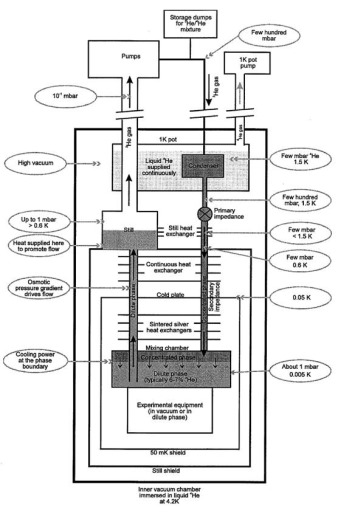
Passons en revue cette partie d’un calculateur quantique. Elle comprend des étages représentés par des disques métalliques sur lesquels sont fixés des fils supraconducteurs et des dispositifs physiques et électroniques de contrôle.
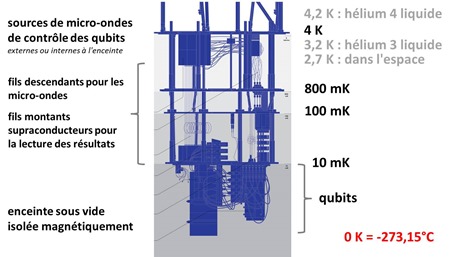
Plus on descend dans les étages, plus il fait froid. Au niveau supérieur, on atteint 4K, soient 4° au-dessus du zéro absolu qui est de –273,15°C. L’échelle de Kelvin démarre au zéro absolu. Cette température où la matière ne bouge littéralement plus est inatteignable. On s’en approche de manière asymptotique. Le record de la température la plus basse est de 450 pK (pico-kelvins) atteinte grâce à l’étonnante technique de refroidissement d’atomes par laser. Dans les ordinateurs quantiques, on se contente d’une température située entre 10 mK et 20 mK (milli-Kelvins). L’étage du dessous est à 800 mK dans cet exemple d’ordinateur quantique IBM. Entre ces deux étage se situe la température la plus basse de l’espace qui est de 2,7 K.
Le refroidissement est réalisé à l’aide de réfrigérateurs à dilution fonctionnant à sec. Ils exploitent de l’hélium liquide avec un flux circulant dans des conduits cylindriques ou en serpentin verticaux reliant les plaques métalliques. Le système fait circuler de l’hélium dans l’ensemble et il n’a pas besoin d’être rechargé régulièrement.
Pour le refroidissement des étages les plus froids, la cryogénie s’appuie sur un mélange d’hélium 4 et d’hélium 3 dont la température de fusion est respectivement de 4,2K et 3,2K. Qui plus est, ils sont tous les deux superfluides aux alentours de 2K.
Le premier est l’isotope d’hélium le plus courant et le plus stable. Le second qui contient un neutron et deux protons est plutôt rare. C’était historiquement un sous-produit du stockage de bombes H à base de tritium, ce dernier se désintégrant progressivement pour produire de l’hélium 3. Il était donc récupéré dans les stocks de bombes H ! Avec les réductions de stocks d’armes nucléaires, la tendance n’est donc pas une production d’hélium 3 à la hausse par ce biais. On peut produire du tritium par irradiation du lithium dans des installations nucléaires spécialisées, comme celles qui sont maîtrisées par le Département de l’Energie US. Actuellement, cet Hélium 3 est produit dans une centrale nucléaire américaine du Tennessee ainsi que dans une centrale nucléaire au deutérium canadienne. La France a des capacités de production de ce type situées notamment dans un réacteur nucléaire expérimental à neutrons du CEA à Grenoble. Mais elle ne les exploite pas forcément pour les ordinateurs quantiques.
Il y a aussi de l’hélium 3 sur la Lune mais il n’est pas très pratique d’aller l’extraire et le récupérer ! Bref, l’hélium 3 est un véritable goulot d’étranglement insoupçonné de la fabrication d’ordinateurs quantiques supraconducteurs ! L’un des moyens d’éviter l’usage de l’hélium 3 est de ne refroidir l’enceinte qu’à environ 1K. Dans ce cas là, on peut se contenter d’hélium 4 pour le circuit de refroidissement.
Le calculateur quantique est placé sous vide et aussi isolé magnétiquement de l’extérieur. Les techniques de refroidissement utilisées sont inspirées de celles des télescopes spatiaux qui opèrent dans l’infrarouge et que nous avions vues l’année dernière dans ma longue série sur l’astronomie. Ces derniers se contentent cependant d’une température de 5K pour le refroidissement des capteurs infrarouges CCD.
Des fils supraconducteurs (ayant une résistance nulle à basse température) relient les qubits à leur système de mesure (donc, dans le sens montant dans le schéma).
L’électronique de contrôle qui opère à la température de 4K doit répondre à un cahier des charges rigoureux. On ne peut pas placer sa carte mère de PC comme cela à cet endroit. Il faut trouver des composants CPU et mémoire qui sont certifiés pour fonctionner à cette température-là. Qui plus est, il ne faut pas qu’ils dégagent de chaleur pour ne pas augmenter la température des qubits. Donc, plus la température de fonctionnement des qubits est basse, moins on peut les contrôler localement avec une électronique de commande. Et réciproquement !
Chez IBM, cette électronique est extérieure à l’enceinte réfrigérée. Mais dans d’autres cas, il semble qu’ils soient dans cette enceinte. Dans les systèmes à supraconducteurs, la partie haute du système contient des systèmes à base de radiofréquences qui contrôlent l’activation des portes quantiques via les fils qui les relient aux chipsets de qubits.
Le schéma ci-dessus, hors commentaires, est issu de Quantum Computers Strive to Break Out of the Lab, 2018.
La photo ci-dessous figure l’intérieur d’un ordinateur quantique d’IBM avec ses rangées de fils supraconducteurs reliant différents étages du calculateur (une partie seulement, celle qui monte, difficile à distinguer des fils descendants de contrôle des qubits). Une visite du laboratoire IBM Q est disponible dans la vidéo A Tour of an IBM Q Lab datant de 2016.
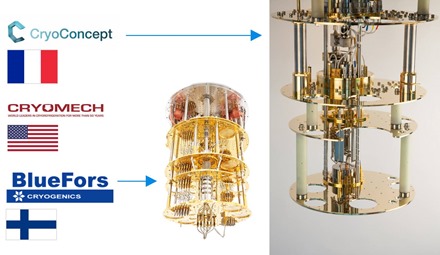
D’où viennent des réfrigérateurs quantiques ? Quelques rares sociétés sont spécialisées dans le domaine, et alimentent aussi bien les laboratoires de recherche que les fabricants d’ordinateurs quantiques. La startup française Cryoconcept est une spécialiste du secteur. Située en région parisienne, elle créé notamment les plateaux de refroidissement, utilisant une technologie provenant du CEA. Ses clients sont essentiellement japonais, français et côté USA, à l’Université de Yale.
Ses principaux concurrents sont les Finlandais BlueFors Cryogenics et l’Américain Cryomech. IBM et Rigetti font appel à BlueFors pour leurs ordinateurs quantiques et D-Wave utilise Cryomech. Les systèmes de cryogénie de CryoConcept ont été testés par différents acteurs dont le CEA à Saclay mais ne semblent pas correspondre aux exigeants besoins de contrôle des ordinateurs quantiques supraconducteurs.
A noter que la taille des plaques métalliques est limitée, ayant un impact sur celle des processeurs quantiques utilisés. Les circuits quantiques doivent aussi être dotés de radiateurs miniatures pour dégager l’énergie générée par les portes quantiques. Selon le CEA, ces radiateurs feraient entre 1 mm et 1 micron de largeur selon Robert Whitney dans Energetics of quantum computing, 2018 (13 slides).
Voici un plan détaillé d’un tel système de cryogénie, reprenant celui d’un prototype d’ordinateur quantique à supraconducteur Oxford Instruments Kelvinox vu dans Improving Coherence of Superconducting Qubits and Resonators (256 pages). Ca ressemble à un système avec compresseur et décompresseur, à ceci près que le fluide utilisé est généralement une combinaison d’Hélium 3 et 4.
Au passage, comment mesure-t-on des températures si basses ? Avec des thermomètres cryogéniques pardi ! J’en ai trouvé chez Lake Shore Cryotronics (source) ainsi que chez Janis (source) qui conçoit aussi des frigos cryogéniques.
Au final, un ordinateur quantique n’est pas bien grand. Dans les laboratoires, le calculateur quantique lui-même tient dans un cylindre d’environ 50 cm de diamètre et environ un mètre de hauteur. L’électronique de commande externe tient dans un à deux racks. Chez D-Wave qui est le seul fournisseur d’ordinateurs quantiques commerciaux, les machines font environ trois mètres cube. C’est plutôt raisonnable compte-tenu de la puissance de calcul qui sera un jour accessible à ces ordinateurs et qui dépassera largement celle de supercalculateurs qui occupent de leur côté de vastes salles blanches.
Mémoire quantique
Evoquons la mémoire quantique ou la qRAM, une mémoire quantique capable de stocker l’état quantique de qubits pour les utiliser ensuite pour alimenter des registres d’ordinateurs quantiques. L’état quantique d’un registre va devoir stocker des qubits en état de superposition.
Avec n qubits, cette mémoire pourra donc stocker en théorie 2 puissance n états différents de ce registre. Elle ne servira pas à stocker autant d’information provenant d’un ordinateur traditionnel mais à conserver l’état d’un registre de qubits d’un ordinateur quantique. Elle est nécessaire à certains types d’algorithmes quantiques comme l’algorithme de recherche de Grover que nous verrons dans la partie suivante. Petit détail de taille : aucune des différentes architectures de mémoires quantiques étudiées depuis deux décennies n’est au point !
Pour en savoir plus sur les basiques de la mémoire quantique, voir par exemple Architectures for a quantum random access memory, des Italiens Vittorio Giovannetti et Lorenzo Maccone et de l’Américain Seth Lloyd, 2008 (12 pages).
Consommation d’énergie
Qu’en est-il de la puissance électrique consommée par l’ensemble ? A ce jour, elle est relativement raisonnable. Un D-Wave consomme environ 15 KW, soit l’équivalent d’une trentaine de serveurs Intel.
Lorsque l’on alignera des milliers de qubits dans ces machines, leur consommation pourra cependant augmenter du fait de l’énergie à dépenser pour maintenir le calculateur à basse température et du coût énergétique de la correction d’erreurs. C’est la thèse de Joni Ikonen, Juha Salmilehto et Mikko Mottonen dans Energy-Efficient Quantum Computing 2016 (12 pages).
Malgré ces écueils, la consommation de grands calculateurs quantiques devrait cependant être largement inférieure à celle de n’importe quel supercalculateur. Un supercalculateur de 2 petaflops de 2009 consommait déjà 6 MW (source). Le supercalculateur le plus puissant du monde début 2018 était le chinois Sunway Taihulight avec une puissance de 93 petaflops et une consommation de 15 MW. On est donc loin de la consommation des calculateurs quantiques actuels et même futurs.
Il est pour l’instant difficile de comparer la puissance d’un supercalculateur avec celle d’un ordinateur quantique mais lorsque les ordinateurs quantiques universels seront opérationnels et qu’ils atteindront la “suprématie quantique” sur un algorithme donné, donc réalisable avec eux mais pas avec des supercalculateurs, leur consommation énergétique restera visiblement inférieure de deux à trois ordres de grandeur (100 à 1000) par rapport à celle des plus grands supercalculateurs. En deux mots, il y a de fortes chances que l’ordinateur quantique soit très efficace d’un point de vue énergétique.
Cout et prix d’un ordinateur quantique
Au vu de la faible maturité du marché, c’est presque une question qui n’a pas de sens. Les seuls ordinateurs quantiques qui sont commercialisés aujourd’hui sont ceux du canadien D-Wave, et à un prix unitaire de $15M.
Le prix d’un ordinateur dépend de plusieurs paramètres dont le coût de fabrication et d’intégration de ses composants, les économies d’échelle, la marge du constructeur, le coût de maintenance et celui d’éventuels consommables. Ce sont des composantes dynamiques : plus le volume de ventes augmente, plus grandes sont les économies d’échelle. Or les volumes sont pour l’instant très faibles. Ils pourraient le rester longtemps jusqu’au jour où des applications émergeront qui toucheront un grand nombre d’utilisateurs et justifieront la fabrication en volume de ces ordinateurs. Il faut bien entendu y ajouter les coûts fixes de la R&D qui sont plus long à amortir si les volumes de vente sont limités.
Reprenons une par une les grandes composantes matérielles d’un ordinateur quantique avec cette analyse d’économies d’échelle :
- L’ordinateur de contrôle : c’est du standard.
- Les composants électroniques de contrôle des portes quantiques : leur technologie dépend du type de qubit utilisé. Dans les ordinateurs supraconducteurs, ce sont des générateurs de micro-ondes.
- Le chipset : celui a beau être fabriqué en technologies CMOS ou avoisinantes, leur volume de fabrication est très faible. Les économies d’échelle sont donc quasiment inexistantes.
- La cryogénie : ce sont des systèmes standards mais commercialisés en faible volume.
- Les consommables : dans les ordinateurs quantiques fonctionnant à très basse température, il y a au minimum de l’azote liquide, de l’hélium 4 liquide (courant) et de l’hélium 3 liquide (beaucoup plus rare et cher). Il semble cependant que ces derniers ne soient pas des consommables et fonctionnent en circuit fermé dans le système de cryogénie.
Par contre, cette liste de composants pourrait rester à peu près stable au gré de l’augmentation de la capacité des ordinateurs quantiques en termes de qubits. Au nez, on peut donc considérer que le prix des D-Wave à $15M puisse rester quelques temps une fourchette haute du prix d’un ordinateur quantique. Ce prix pourra décroître au gré de l’accroissement du volume de production, qui dépendra étroitement des usages.
Dans la pratique, nombre d’ordinateurs quantiques seront utilisables comme des ressources dans le cloud et avec un coût plus modéré. C’est ce que proposent déjà IBM, Rigetti et D-Wave et proposeront Google et Microsoft. Seul Intel pourrait être amené à vendre des ordinateurs ou des processeurs sans les proposer dans le cloud. Et encore, on n’en sait vraiment rien !
Pour en savoir plus
J’ai consulté un très grand nombre de sources d’informations pour réaliser cette partie, à la fois côté recherche et côté fournisseurs comme chez IBM ou D-Wave. A noter Quantum Computing Gentle Introduction du MIT, publié en 2011 (386 pages) qui décrit avec précision certains mécanismes des ordinateurs quantiques comme les méthodes de lecture de l’état des qubits. Il décrit aussi assez bien les fondements mathématiques utilisés dans les calculateurs quantiques. Vous pouvez aussi profiter d’une vidéo de 8 minutes d’un beau gosse américain, Dominic Walliman, qui vulgarise bien les basiques de l’ordinateur quantique !
__________________________________
Maintenant que nous avons désossé les ordinateurs quantiques d’aujourd’hui, il nous faut maintenant étudier ce que l’on fait avec ! C’est l’objet de la partie suivante consacrée aux algorithmes et applications quantiques. Je l’ai déjà découpée en plusieurs parties avec une première consacrée aux algorithmes et principaux usages, une sur les limites théoriques de l’informatique quantique, une sur les outils de développement et une dernière sur les applications sectorielles du quantique.
![]()
![]()
![]()
Reçevez par email les alertes de parution de nouveaux articles :
![]()
![]()
![]()































 Articles
Articles
Allez, on continue son cours sur l’informatique quantique !merci @olivez https://t.co/DivSQUF6Sr
Excellente introduction et j’ai presque tout compris ! Je découvre que la mise en œuvre de cette technologie est d’une complexité effroyable
Complexe, oui et non.
Si j’étais rentré dans les détails du fonctionnement d’un processeur traditionnel d’aujourd’hui, type Intel, cela aurait aussi été très compliqué à piger. Il se trouve qu’on les utilise avec des outils de développement accessibles quel que soit le langage de programmation utilisé. Et les usages qui vont avec ne requièrent pas de comprendre comment le matériel fonctionne.
Pour le quantique, on doit se contenter d’en comprendre les couches basses. C’est aussi vrai de la programmation que nous verrons dans l’épisode suivant. Comme si on ne pouvait programmer un ordinateur d’aujourd’hui qu’en assembleur, ce qui serait quelque peu rébarbatif !
Bref, oui, il faut s’accrocher. Mais quand le sujet sera plus mature, cela sera moins nécessaire !
Pour enfin comprendre comment fonctionne un ordinateur quantique, un nouvel article d’Olivier Ezratty… https://t.co/Fb2ETf34px
Merci Olivier pour cet excellent article démystification
PS : je parle de cet article.
https://t.co/wwggpk0EVH
Je potasse depuis un mois vos fiches, c’est passionnant. Merci pour ces explications claires et les schémas fournis permettant de mieux comprendre le fonctionnement et les bases de l’informatique Quantique.