In the quantum computing realm, there’s often some confusion with simple technical lingua.
For example, in many general audience publications, you can read that ‘quantum cryptography’ is one application of future quantum computers. As a matter of fact, in a very distant future, quantum computers may break some RSA-based cryptography keys, but not create safer cryptographic systems. ‘Quantum cryptography’ is about creating shared encryption keys with quantum links that do not use quantum computers, and in most cases today, not even quantum entanglement, using the BB84 QKD protocol or one of its many variations. Quantum Key Distribution is indeed in the field of quantum cryptography. One right wording for the role of quantum computers here would be to associate them with ‘cryptanalysis’, the set of techniques used to break cryptographic security.
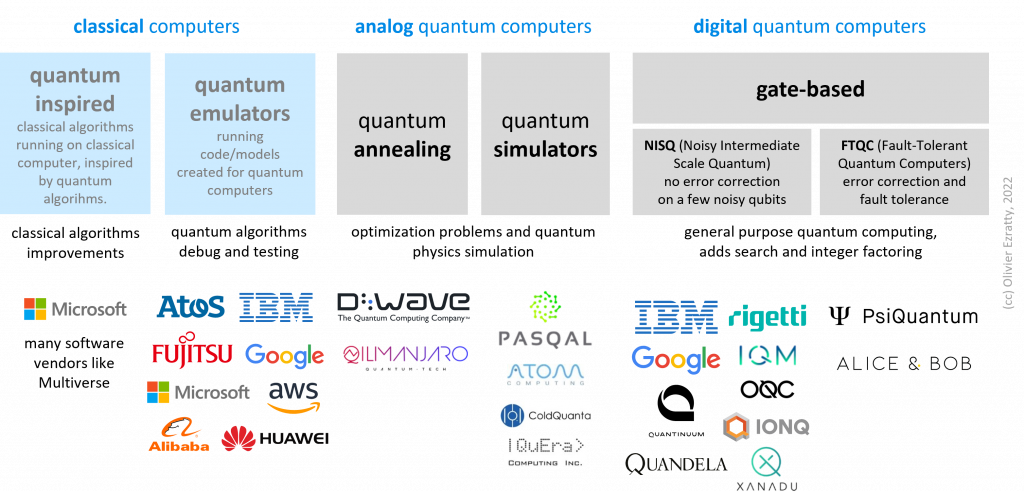
The confusion that is covered here is about quantum emulation vs quantum simulation. There is no shared agreement on how to name these things, although quantum simulation is frequently used indifferently to cover many of the different concepts described in this text.
Quantum emulators
These are combinations of classical software and hardware that can execute quantum algorithms and code that are designed to run on quantum computers, particularly when it takes into account the specifics of some quantum computer hardware. The classical computers can range from simple laptops to supercomputers, depending on the number of qubits to be emulated. The classical memory required for emulation doubles as you add one qubit. Also, the longer the quantum code, the longer it will take to emulate. I’m using here the “quantum emulator” descriptor, which corresponds to the classical view of an emulator, which runs some software code on one machine that was designed for some other hardware, usually older.
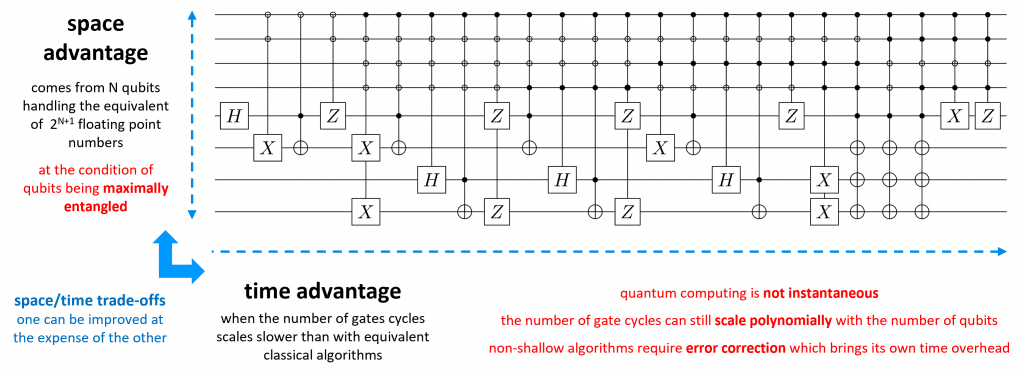
We must differentiate here the space and time potential advantages of quantum computing. These are a bit like the size of your computer memory that complements the speed of your processor and length of your code. However, there’s always a trade-off that is valid with quantum computing: the more memory you have (here, in number of qubits), the faster your problem can be solved, and vice-versa. Still, the quantum computing space advantage enables parallelism in many algorithms like Grover and is a source of speedups. But the speedup itself depends a lot on the algorithm design, which can be for example polynomial (Grover) or exponential (QFT, Shor, …). Still, quantum parallelism make use of the space advantage like when a given function can be simultaneously evaluated on all amplitudes within a quantum register like in Grover’s and all oracle-based algorithms.
Quantum emulators execute quantum code with the processing capabilities of traditional computers, using large vectors and matrices computing. Indeed, qubit operations are relatively simple vector/matrix operations using floating point numbers! Single and two-qubit gates are emulated with applying 2×2 or 4×4 complex number matrix multiplications on a vector representing the quantum computer qubit register state vector.
Quantum code emulation serves multiple purposes among which:
- Learning how to code with cheap classical computing resources, including your own laptop (like with using Quirk).
- Visualize a quantum algorithm internal data which can’t be easily done with a real quantum computer due to the qubit state collapse provoked by their measurement, suppressing superposition and entanglement.
- Develop new quantum algorithms and test them at a low scale.
- Verify that a quantum algorithm is generating the expected results, also at a low scale.
- Design and test error correction codes à low scale.
Quantum emulators are sometimes called quantum simulators or classical quantum simulators (like with IonQ), but this naming should be avoided to prevent the confusion with… quantum simulators. Quantum simulators are analog quantum computers simulating many-body quantum physics phenomena, as envisioned by Richard Feynman in 1981, in Simulating Physics with Computers.
Quantum emulators may however also work at different levels. The most classical ones are emulating perfect mathematical qubits which have no defects and zero error rates. Others can add simple noise effects on calculations to see their impact on algorithm, compared to having no noise. At last, more sophisticated emulators can also reproduce the (quantum) physical characteristics and defects of various qubits and in that case, they also implement some form of ‘digital quantum simulation’ of the qubit internal quantum dynamics. This is more or less what Quandela Perceval does for its photon qubits with modelling the effect of light devices like beam splitters, polarizers and Mach-Zehnder interferometers. Qiskit Metal from IBM is a different tool. It helps design a superconducting qubit and run physical simulations, but not up to the point to run quantum code on it.
To date, supercomputers can fully emulate up to 55 qubits. Records have however been broken with more than 100 qubits emulations, with a low number of quantum gates and using various compression techniques using the likes of “tensor networks”. Emulating quantum computer code requires a lot of power both on the memory side, to store and compute the 2N complex amplitudes from a quantum register of N qubits, if not the full 22N real numbers of the register density matrix that is useful to simulate qubit noise models and the effects of decoherence, and for the associated processing that relies on floating-point matrix multiplications. Still, records in this field are regularly broken with using various compressing techniques, such as the one described in the preprint A density-matrix renormalization group algorithm for simulating quantum circuits with a finite fidelity by Thomas Ayral, E. Miles Stoudenmire, Xavier Waintal et al, August 2022. The paper shows that with noisy qubits, quantum emulation costs scales only polynomially with the number of qubits. On top of this, they could emulate Google’s 53-qubit 2019 supremacy experiment on a Atos QLM occupying half a rack and on one processor core, in 8 hours (vs less than 3 minutes for Sycamore).
We can also compare the resource constraints and computing time with running the same quantum algorithm on an existing quantum computer and a classical computer emulating it. With a small number of qubits, the performance may be better with a classical computer and as the qubit number grows, it usually plays to the advantage of the quantum computer. But, unfortunately, there are very few benchmarks comparing these two scenarios for a given quantum algorithm.
A quantum system performing better than its classical emulator counterpart wouldn’t mean we are yet in the quantum advantage regime. This would happen if the quantum computer clearly exceeds the performance of a classical computer running the best-in-class classical algorithm to solve the given problem. A best-in-class algorithm is probably more efficient than running an emulation of the quantum algorithm used for the comparison even if it is running some form of “quantum inspired” algorithm using tensor networks.
At last, let’s mention the fact that a quantum emulator like Atos’s QLM can emulate the operations of all quantum computing paradigms, so not only gate-based quantum computers but also quantum annealers ala D-Wave and quantum simulators ala Pasqal and QuEra. In that case, you have a (classical) quantum emulator emulating a quantum simulator, itself simulating a quantum system. Got it?
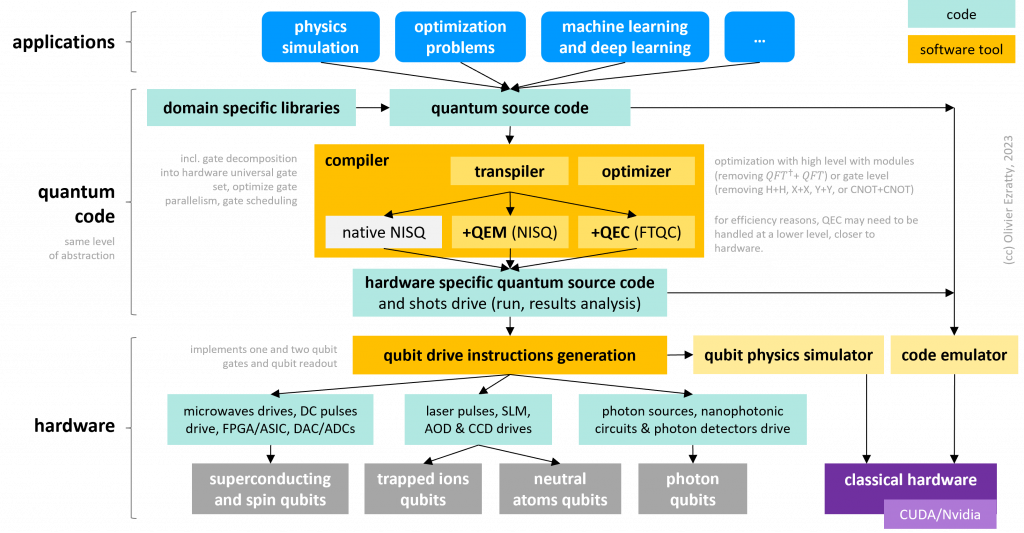
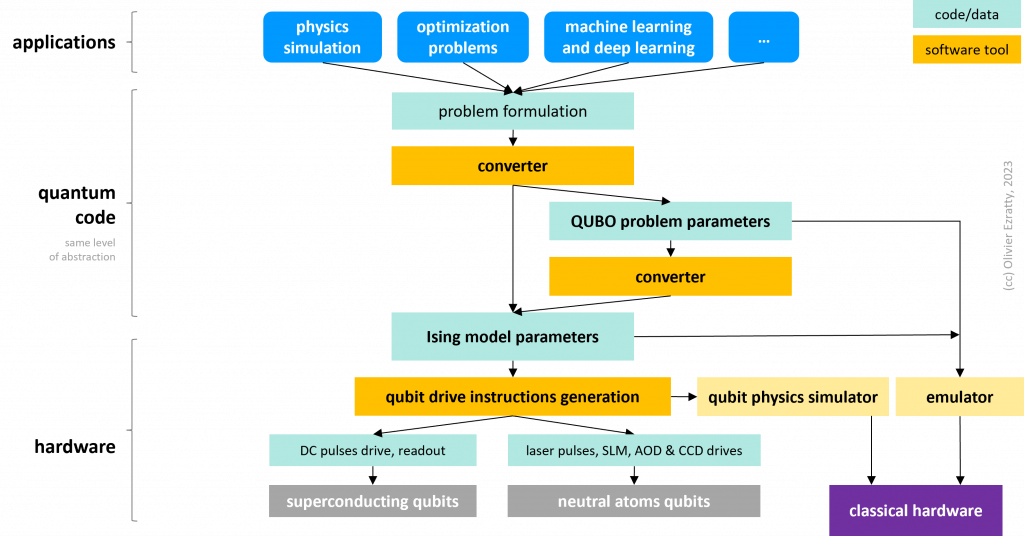
Looking at the whole quantum computing software stacks, where is the emulator? The above chart tries to explain the thing.
First, let’s describe what a quantum compiler usually does. It does not really convert a given programming language (like a C or C++ in classical computing) into some lower abstraction-level machine language directly executable by a quantum computing system (like assembly or machine language in classical systems). Quantum compilers can use some regular OpenQASM code and convert it in… OpenQASM code. There may still be some language conversion if Python is used for example with the Qiskit framework to create program loops and the likes. Compilers can implement many features like transpiling the gates used in the code to primary gates available on your target quantum computer. It can optimize the code and remove redundancies like two consecutive H gates which are equivalent to doing nothing and reduce the number of costly gates like SWAP (which switches two adjacent qubit values are are used a lot when qubit connectivity is limited) and T gates (one eighth of a phase turn in Bloch’s sphere, and the key primitive gate to generate arbitrary phase rotation gates). It can also optimize the gate flow with taking into account the specifics of your quantum hardware and qubit connectivity. By the way, let’s notice that quantum code compiling and optimizing is an NP-complete problem, as described in On the Complexity of Quantum Circuit Compilation by Adi Botea et al, IBM Research in 2018. It means that the compiler task complexity grows exponentially with the code size which has to be taken into account for code designed for thousand of (logical) qubits.
Even if it was converting a code with logical qubits into physical qubits and use quantum error correction codes, in the end, you’d still have qubit gates at the same level of abstraction. The difference would be at the level of the qubit fidelities. However, the positioning of quantum error correction in the above graph may be wrong practically. Quantum error correction will probably require some dynamic programming and to run it at a lower level, much closer to hardware and qubit control.
Real “compilation” with a change of abstraction level usually happens elsewhere in the software food chain and it is invisible to quantum software developers. It happens when the optimized/transpiled gate instructions are converted into electronic instructions to drive physical qubit operations, like described at the bottom of the above chart. It is often implemented in the qubit drive electronic systems like those from Quantum Machines or Zurich Instruments, Qblox and Keysight. These are independent systems from compilers/transpilers/optimizers.
In Understanding Quantum Computing, 2022 edition (free PDF and paperback on Amazon), I provide a 5-page inventory of the tens of quantum emulators available, mostly in open source. Hardware wise, the most common solutions are the QLM from Atos and the DGX servers from Nvidia implementing their cuQuantum SDK. Cloud vendors like Google, Microsoft, Amazon and even IBM all have some quantum emulation software offering with a variable support in number of qubits. IBM Qiskit Aer is the Qiskit emulator available online in IBM Quantum Experience environment. OVHcloud is also about to make an Atos QLM emulator available on its cloud offering.
Quantum simulators
These are different beasts than emulators. They belong to a specific breed of quantum computing systems and quantum computing paradigm. They are used as simulators of quantum phenomena without using gates-based qubit systems. They are also called “many body systems”. They work in an analog and not digital way, i.e., the parameters linking the qubits together are continuous. Even though I’d say that gate-based quantum computers are still analog systems during computation.
The most commonly used quantum simulation technique is based on neutral atoms that are cooled and controlled in ultra-vacuum by lasers, like the ones from Pasqal (France) and QuEra (USA). Trapped ions, superconducting qubits, spin qubits and other qubit types could also be used for running quantum simulations but no commercial vendor is promoting it when they can also implement gate-based quantum computing which is supposed to be more generic. But more long term with respect to commercial viability.
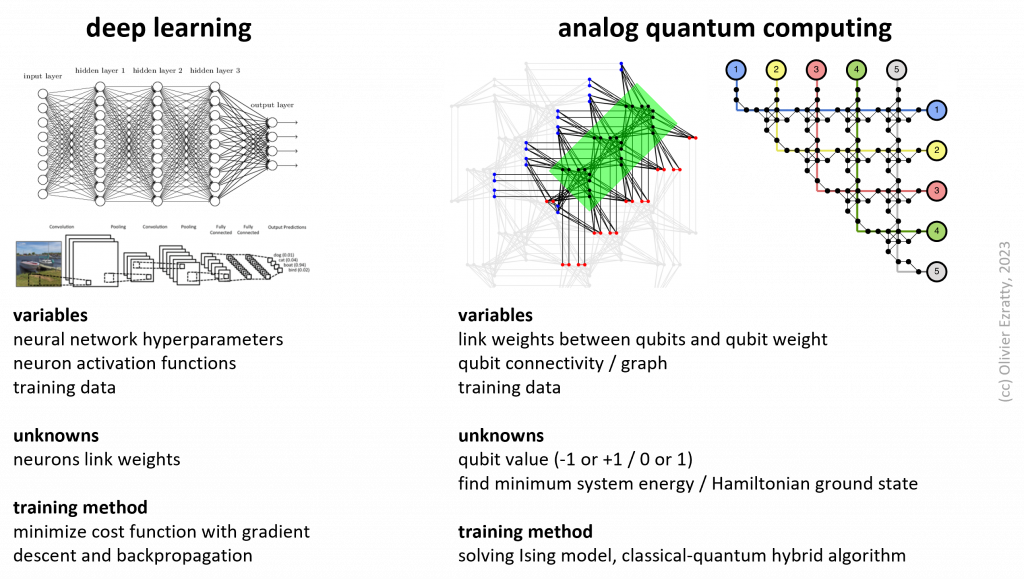
In the case of analog quantum computing emulation, the process is a bit different with analog quantum computers. Analog quantum systems are programmed in a different way. Neutral atom quantum computers are often presented as “programmable Hamiltonian systems”. Their vendors do not like their weird positioning vs gate-based quantum computers. But this programming takes place classically.
It consists in preparing an Ising model which looks like a neural network where the variables are the connections between the qubits and their weight, and the searched unknowns are the qubit values (0 or 1, or -1 or +1). There is no compilation per se in the process but a series of problems conversion. We can start with an optimization business problem and convert it to a QUBO problem, a generic way of describing an binary optimization problem. They, some software layer converts this problem into an Ising model problem that is solvable by your quantum simulator or quantum annealer. There are some variations between these, given the qubit topology is more flexible with quantum simulators. Neutral atom based quantum simulators can also implement other modes than solving Ising models like so-called XY Hamiltonian models with more degrees of liberty.
Practically speaking, most gate-based quantum algorithms have some equivalent for analog quantum computers, including quantum simulators. This is the case of course for physics simulations and that was the initial intent from Richard Feynman. It also works with many optimization problems, with quantum machine learning, with partial differential equations, with Monte Carlo simulations and the likes. The only gate-based algorithms that seem to not fit into simulation models are searches (like those done with Grover’s algorithms) and integer factoring (ala Shor algorithm).
There’s another naming circulating around: digital quantum simulators. These are classical systems able to simulate the physics of some quantum system. They are currently used to run quantum chemistry simulations, particularly in drugs discovery research. It can also relate to a gate-based algorithm simulating a many-body quantum system.
Now, how can we emulate a quantum simulator? There are a few tools around lile MyQLM from Atos, which supports this on top of emulating gate-based and quantum annealing systems. Pasqal launched Pulser in 2021, jointly with the Unitary Fund, which supports emulating qubit controls at a low level in their neutral atoms quantum simulator.
Quantum inspired
Let’s also mention quantum inspired computing which is about using classical algorithms running on classical hardware that are inspired by quantum algorithms and bring some new efficiencies. They are not about emulating quantum code on a classical computer. Typical quantum inspired algorithms use tensor network libraries (in simple wording, performing various matrix multiplications in an optimized way).
But there is a connection between quantum inspired algorithms and quantum emulators of gate-based quantum computers. These quantum emulators use a lot ot tensor networks which optimize the computing of gate operations. The same tensor networks that are used in quantum inspired classical algorithms!
Quantum emulation resources
The required classical computing capacity grows more or less exponentially with the number of supported qubits. On a laptop equipped with 16 GB of memory, you can emulate about 20 qubits in gate-based mode.
Specialized server appliances such as Atos’ QLM fits in a datacenter rack, are designed to manage a very large amount of memory and can support the emulation of up to 40 qubits. More than 40 qubits can be emulated on massively parallel architectures and supercomputers or on a large number of clusters.
There are various methods for emulating a circuit of N qubits and a certain level of depth of quantum gate sequences which will resonate with what we’ve learned about registers computational basis and density matrices. We’ll cover some of them from the hardest to the simplest with regards to computational resource requirements.
- Density matrix computing which requires 2Nx2N complex numbers, so 22N+1 floating point numbers. It is the most memory-hungry method and is not used with a large number of qubits. It can be necessary if you need to emulate imperfect qubits with their noise and decoherence and their impact on quantum algorithm’s execution. It can also help design quantum error correction codes adapted to specific qubit noise models.
- Quantum state vector which handles the complex amplitudes of all the Hilbert space managed by N qubits in memory. It requires 2N complex numbers representing 2N+1 floating point numbers and 2N+5 bytes with double precision floating point numbers using 16 bytes. The action of quantum gates on this large vector consists in applying to it the quantum gates unitary matrices to one, two or three qubits which are respectively made of 2×2, 4×4 or 8×8 complex numbers. This method is implemented on supercomputers with huge memory capacities of the order of several Po. It is currently limited to about 50 qubits.
- Tensor network compression techniques are used to simplify emulation and ease its distribution across multiple classical computing nodes. It was used for example in September 2019 by Alibaba on a cluster of 10,000 servers with 96 CPUs. They simulated Google Bristlecone’s 70 qubits (which never did really run practically) over a depth of 34 quantum gates with 1449 instances of their Cloud Elastic Computing Service (ECS), each comprising 88 Intel Xeon chipsets with 160 GB of memory. So, a total of 127,512 processors! This method can be implemented with many compression techniques providing a lower accuracy. It was improved in October 2021, again by Alibaba, to classically simulate the Google Sycamore on the new Sunway supercomputer in 304 seconds.
The main limitations of supercomputers for emulating quantum algorithms are more related to their memory (RAM) than to their processing capacity. It would take about 16 Pb of memory to fully simulate 50 qubits. How about 96 qubits? The memory requirement would be multiplied by 246+1 (+1 for the complex number representation over 2 floating point numbers). Moore’s law with memory cannot therefore keep pace with a linear increase of the number of used qubits in a quantum computer.
Beyond emulation
Quantum code emulation works as far as classical computers can cope with the number of emulated qubits and the size of the algorithm. What can we do beyond this limit? At this point in time, it’s not a big deal since no available quantum computer is really beyond the reach of quantum emulation. Theoretically, it could be the case for Rigetti’s Aspen 80 qubit systems, IBM’s 127 and 433 qubit QPUs, but practically, these systems are so noisy that they can’t be used beyond very shallow algorithms that can be emulated to some extent.
For real complicated algorithms requiring hundred to thousand (logical) qubits, you can just try to estimate the hardware resources that would be required to run it, including error correction overhead. That’s what Microsoft’s Resource Estimator published in November 2022 does. It targets FTQC (fault-tolerant quantum computing) applications and estimates the needs in physical qubits and qubit gates based on the algorithm itself and on the qubit figures of merit (fidelities, gates, size). The tool was used by Alice&Bob to evaluate in a post the number of qubits required to factorize a RSA 2048 bit encryption key with Shor’s algorithm. The result end up being 130K physical cat-qubits. See Assessing requirements to scale to practical quantum advantage by Michael E. Beverland et al, Microsoft Research, November 2022 (41 pages).
Next in line would be to also assess (and optimize) the energy consumption and power requirements for a quantum computer running a given algorithm, a key topic for the Quantum Energy Initiative.
Summary
A quantum emulator is able to run some quantum code or quantum analog model on a classical computer. It is based on specific software and generic or specific hardware depending on the size of the code/model to emulate. The more powerful the hardware in memory and processing capacity, the larger the number of qubits that can be emulated.
A quantum simulator is a specific category of analog quantum computer that can directly use many-body quantum physics to simulate by analogy the physics of other quantum physical systems and solve many other categories of problems.
A digital quantum simulator is a classical computing solution used to simulate the physics of some quantum system. It is typically used for quantum chemical simulations using algorithms based on DFTs. It can also be used to digitally simulate the physics of a qubit.
But I know these definitions are not agreed upon in the industry. Google, IBM, Amazon, Nvidia all used “simulator” in place of “emulator”. See also the interesting debate with Jack Krupansky on LinkedIn (in the comments section).
Oh, and by the way, don’t trust ChatGPT too much for this matter. It is a bit lost as the dialog below shows, done with OpenAI Playground.
Short bibliography
Richard Feynman, Simulating Physics with Computers, 1981.
Thomas Ayral, E. Miles Stoudenmire, Xavier Waintal et al, A density-matrix renormalization group algorithm for simulating quantum circuits with a finite fidelity, 2022.
Atos, MyQLM documentation.
IBM, Qiskit Aer emulator.
Pasqal, Pulser: a control software at the pulse-level for Pasqal quantum processors, 2021.
Quandela Perceval open source emulator.
Adi Botea et al, IBM Research, On the Complexity of Quantum Circuit Compilation, 2018.
Olivier Ezratty, Understanding Quantum Computing, 2022 edition, 2022.
Michael E. Beverland et al, Microsoft Research, Assessing requirements to scale to practical quantum advantage November, 2022.
Alice&Bob, Alice & Bob tests Azure Quantum Resource Estimator, highlighting the need for fault-tolerant qubits, 2022.
![]()
![]()
![]()
Reçevez par email les alertes de parution de nouveaux articles :
![]()
![]()
![]()





























 Articles
Articles
Digital quantum simulation has another sense in the quantum physics community. It corresponds to the implementation of an algorithm aiming at reproducing a quantum model of interest (quantum simulation) using gate-based circuits (digital). See for example https://www.nature.com/articles/s41534-019-0192-5 or https://fab.cba.mit.edu/classes/862.22/notes/computation/Lloyd-1996.pdf