Pour ce 38e épisode des entretiens Decode Quantum et le premier enregistré en 2022, Fanny Bouton et moi-même recevions Daniel Esteve, du CEA. Ces entretiens sont toujours également diffusés par Frenchweb.
Il est physicien et Directeur de recherche au CEA. Il était responsable du groupe Quantronique au CEA de Saclay qu’il a créé en 1984 avec Michel Devoret (Decode Quantum 23) et Cristian Urbina. Ce groupe travaille sur la conception et l’utilisation de circuits électriques avec effets quantiques dans le vaste champ de la matière condensée et de la physique mésoscopique, qui porte sur l’étude de la matière à des échelles allant de l’atome au micromètre. En langage courant, Daniel est un pionnier des qubits supraconducteurs dont nous raconte un bout de leur longue histoire.
Cette histoire est typique de ce qui peut se passer dans la recherche fondamentale, avec des débuts qui n’ont rien à voir avec la suite, et réciproquement. Les recherches en physique mésoscopique des années 1980 ont progressivement mené à la création de capteurs supraconducteurs et de qubits mais c’est venu progressivement. C’est aussi le fruit d’un travail international impliquant de nombreuses équipes de recherche, en France, aux USA, en Suisse et au Japon, pour ne citer que les principaux pays impliqués. Les Google et IBM qui ont ensuite massivement investi dans les qubits supraconducteurs se sont appuyés sur des décennies de recherche fondamentale amont. Et comme le précise bien Daniel, ce qu’ils font aujourd’hui relève encore pour une bonne part de la recherche fondamentale.
D’ailleurs, on retrouve dans l’histoire un certain John Martinis, qui a été un temps post-doc de Daniel Esteve au CEA de Saclay, bien longtemps avant de superviser la recherche en calcul quantique de Google côté hardware entre 2014 et 2020. Sans compter Michel Devoret, qui joue un rôle clé dans la recherche sur les qubits supraconducteurs à l’Université de Yale et qui avait notamment accueilli Mazyar Mirrahimi d’Inria au début des années 2010, ce dernier étant le pionnier des “qubits de chat” exploités par la startup française Alice&Bob.
Voici un synopsis des points évoqués avec Daniel Esteve dans cet entretien :
- Côté études, Daniel Esteve est passé par l’ENS Saint-Cloud, est ensuite devenu agrégé de sciences physiques puis et docteur ès sciences.
- Il a réalisé sa thèse dans le laboratoire d’Anatole Abragam au CEA. Elle qui portait sur la mise en évidence de phases de type verre orientationnel dans des solides moléculaires avec des méthodes RMN originales. Cela fait partie du champ de la résonance magnétique nucléaire (RMN) et des verres de spins. Il évoque les premiers processeurs quantiques réalisés avec le contrôle de spin de molécules. Il évoque le post-doc qu’avait fait Michel Devoret à Berkeley chez John Clarke, un physicien britannique notamment connu pour sa contribution dans la création de capteurs supraconducteurs de type SQUID.
- Puis nous parlons d’Anthony Leggett et de son intuition. Il se demandait si la physique quantique s’appliquait à des systèmes macroscopiques, ici, de multiples paires d’électrons dites de Cooper, qui se forment dans des matériaux supraconducteurs à très basse température. Et d’Anton Zeilinger à Vienne puis de la création de la cQED (circuit Quantum Electro Dynamics) par Andreas Wallraff et Rob Schoelkopf.
- Il raconte l’histoire du groupe Quantronique et, indirectement, celle des qubits supraconducteurs, qui commence par une recherche amont très fondamentale sur la physique mésoscopique, la matière condensée, les atomes artificiels. Il évoque l’expérience de la fin des années 1980 qui avait permis d’observer l’effet de la dissipation sur l’effet tunnel quantique macroscopique dans les jonctions Josephson.
- C’est la période de la physique des petites jonctions, initialisée par le Russe Konstantin Likharev (voir Theory of the Bloch-wave oscillations in small Josephson junctions par D.V. Averin, A.B. Zorin et K.K. Likharev, 1985) puis avec l’expérience de Theodore Fulton et Gerard Dolan sur le transistor à un électron et l’utilisation de deux jonctions tunnel en série (voir Observation of single-electron charging effects in small tunnel junctions par T. A. Fulton and G. J. Dolan, 1987). Daniel nous parle aussi les écluses et pompes à électrons et de la thèse de Hughes Pothier (“Blocage de coulomb et transfert d’électrons un par un”, 1991).
- Il évoque aussi le rôle de John Martinis post-doc pour les expériences d’effet Josephson alternatif qui ont prouvé l’appariement électronique dans les supraconducteurs à haute température critique, entre 1985 et 1987, en même temps que la mesure par Jaw-Shen Tsai du quantum de flux dans ces matériaux.
- On couvre alors le blocage de Coulomb, une île connectée en réservoir à une jonction Josephson et une capacité. C’est une boîte à électrons qui exploite un transistor à un électron pour la mesure. Cette prouesse est citée par Steve Girvin de Yale dans une vidéo d’août 2021. Cela aboutit à la thèse de Vincent Bouchiat en 1997 (voir Fluctuations quantiques de la charge dans les circuits a un electron et a une paire de Cooper).
- Puis le rôle de Yasunobu Nakamura de NEC et de la première expérience de 1999 (avec Yuri Pashkin and Jaw-Shen Tsai) de manipulation de l’état quantique d’une boîte à paires de Cooper avec une irradiation de micro-ondes. Cette expérience montre les oscillations de Rabi entre deux états quantiques. C’est une preuve de la superposition quantique cherchée depuis longtemps pour un système non microscopique. La notion d’oscillations de Rabi qui correspond à deux états quantiques en couplage alternatif.
- A l’époque, le temps de vie du qubit était court, de quelques ns. C’était un circuit quantique très simple avec une superposition entre états de charge.
- Le besoin de lire l’état quantique a amené au quantronium qui assurait une meilleure protection contre la décohérence. Et avec une mesure de l’état quantique de la jonction Josephson en un coup avec une bonne fidélité. L’expérience du CEA a été proposée en 2001 et publiée en 2002.
- Ils ont ensuite essayé de créer un circuit à 2 qubits. Cela n’a pas bien marché. Il était difficile de lire l’état quantique.
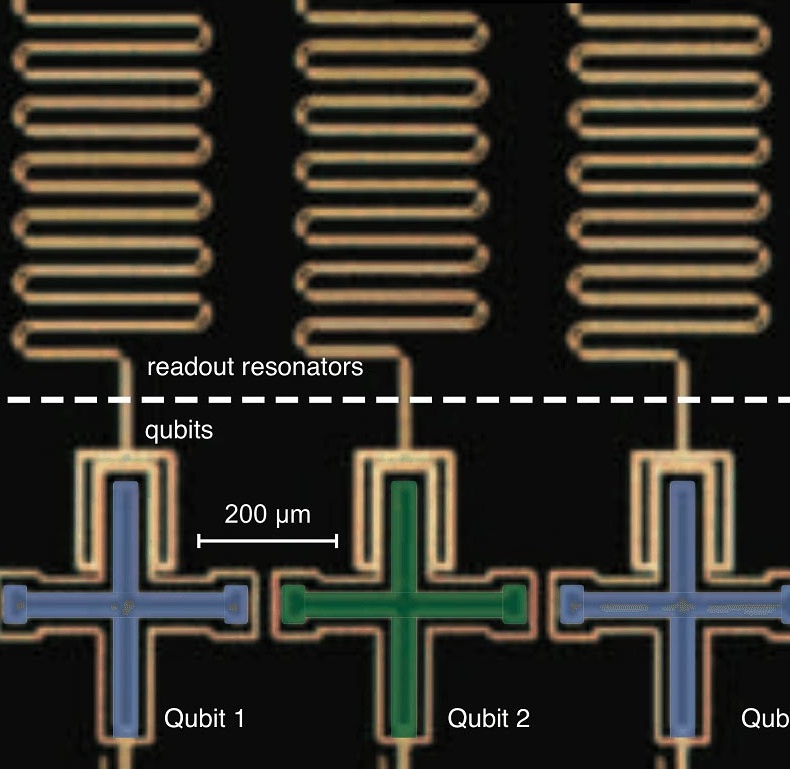
- Une nouvelle version de boîte à paires de Cooper plus performante a été développée à Yale en 2004 par Rob Schoelkof et son postdoctorant Andreas Wallraff (maintenant à l’ETH Zurich). L’idée consistait à coupler une boîte à paires de Cooper à un résonateur micro-ondes en forme de trombone à coulisse (exemple ci-dessous), une technique inspirée de l’électrodynamique des atomes en cavité étudiés par Serge Haroche.
- Cela a abouti à la version la plus courante des qubits supraconducteurs, le transmon entre 2006 et 2007. Les paires de Cooper sont placées dans un régime proche de l’état de phase, proche d’un oscillateur harmonique. La première lecture d’un transmon à haute-fidélité a été réalisée en 2009. La Quantronique réalise en 2011 un premier processeur quantique à deux qubits complètement fonctionnel. Ce processeur permet d’exécuter l’algorithme de recherche quantique de Grover (thèse de Andreas Dewes), et d’obtenir une preuve de principe de l’avantage quantique. Un processeur de 4 qubits est ensuite réalisé en 2015. Voir Design, fabrication and test of a four superconducting quantum-bit processor par Vivien Schmitt, 2015 (192 pages) mais la Quantronique abandonne cette voie pour la montée en échelle.
- Cette voie est notamment poursuivie chez IBM, Google et Rigetti. En parallèle étaient développés de codes de correction d’erreurs mais nécessitant une fidélité des qubits supérieure à 99%, ce qui n’est pas facile à obtenir à grande échelle.
- On parle de la voie alternative consistant à réaliser des qubits plus cohérents ou déjà corrigés pour rendre la correction d’erreur quantique moins difficile.
- On parle aussi de qubits supraconducteurs au tantale qui ont moins de décohérence et tiennent entre 500 μs et 1 ms (vs les moins de 100 μs actuels). Des équipes chinoises ainsi que Jay Gambetta chez IBM travaillent dessus.
- Nous évoquons aussi les mémoires de spin utilisables dans des répéteurs et leur usage pour exploiter des processeurs avec moins de qubits.
- La fabrication des qubits supraconducteurs dans une nouvelle salle blanche à l’usage de toute la communauté des circuits quantiques supraconducteurs, financée par le plan quantique national, et qui sera installée au CEA à l’Orme des Merisiers.
Bientôt, je vais pouvoir utiliser toutes ces informations pour reconstituer une timeline complète de l’histoire des qubits supraconducteurs ! Pour l’édition 2022 de mon bouquin ‘Understanding quantum technologies’ ! Cela pourrait prendre la forme d’une sorte de “FBI wall” du domaine. Et ses ramifications sont très nombreuses !
![]()
![]()
![]()
Reçevez par email les alertes de parution de nouveaux articles :
![]()
![]()
![]()





























 Articles
Articles
ATTENTION DE DANIEL ESTEVE
Bonjour Daniel,
J’espère que tu vas bien malgré ces temps plutôt troublés (et c’est un euphémisme…)
Daniel, je me pose une question toute simple sur laquelle je pense avoir un peu avancé ces derniers temps. Et j’aimerais avoir ton avis sur le point de départ.
Considère un qubit défini par son Hamiltonien H(t) dans un environnement extérieur donné. Son énergie moyenne est bien sûr E(t) = avec Psi(t) fct d’onde du spineur.
On peut alors définir l’opérateur “variance” hermitien:
V(t) = [H-E]² et, donc, l’écart-type correspondant:
\sigma(t) = \sqrt[] .
Question : à ton avis, est-ce physiquement raisonnable? Et, si oui, y a-t-il une relation et/ou une redondance avec des travaux déjà bien connus sur cette détermination quantique de la variance d’un système quantique et de son écart-type?
Tu vois, je continue à caresser à rebrousse-poil les systèmes quantiques (à deux niveaux: je connais mes limites…) !
Cela me ferait bien plaisir de te revoir. Si par hasard tes pérégrinations te conduisent vers la Côte d’Azur et Nice… Sinon, 1 de ces 4 à Paris?
Bien amicalement à toi, Daniel,
et amical bonjour de ma part également à Michel D. si par hasard tu le rencontres.
Gilbert
Euh, Daniel, il y a des erreurs de typo indépendantes de ma volonté, dus à mon écriture sous forme de bras et de kets!…
Il faut lire bien sûr: E(t) = ProdScal de Psi* avec H Psi,
soit: E(t) = (Psi* . H Psi) ,
et idem: \sigma(t) = \sqrt[ProdScal de Psi* avec V Psi] :
\sigma(t) = \sqrt[(Psi* . V Psi)] .