Le 3 décembre 2020, les équipes de Chao-Yang Lu de l’USTC (University of Science and Technology of China) de Shanghai sous la coupe du tsar du quantique chinois Jian-Wei Pan annonçaient avoir battu un record d’avantage quantique avec une expérience de photonique impressionnante. La communication chinoise étant plus extravertie que celle d’une expérience voisine d’octobre 2019 qui avait été quelque peu éclipsée par l’annonce de la suprématie quantique de Google, elle est plus visible et relayée par les médias du monde entier. L’expérience a même un nom à retenir : Jiuzhang.
Les performances annoncées de cette expérience chinoise peuvent paraître ébouriffantes. Mais qu’en est-il d’un point de vue pratique ? En quoi consiste-t-elle et quels horizons ouvre-t-elle en termes de calcul quantique ? Plus généralement, comment évaluer la puissance d’un calculateur quantique ? Après un descriptif de cette prouesse chinoise, nous allons ici traiter des outils de benchmarking de calculateurs quantiques. Tout d’abord avec le volume quantique qui est promu par IBM depuis 2017 et adopté depuis 2020 par Honeywell et IonQ, puis en évoquant l’intéressante annonce du benchmark Q-score faite par Atos le 4 décembre 2020.
Bref, voici un texte destiné à traiter largement de cette épineuse question du benchmarking et de la comparaison des calculateurs quantiques entre eux et avec les supercalculateurs les plus puissants du monde.
L’échantillonnage de boson gaussien chinois de 2020
Il est décrit dans la publication scientifique Quantum computational advantage using photons par Han-Sen Zhong et al, 3 décembre 2020 (9 pages) et dans des abondants supplemental materials associés (64 pages). Le contenu de l’expérience est assez bien vulgarisé dans Light-based Quantum Computer Exceeds Fastest Classical Supercomputers par Daniel Garisto dans Scientific American, décembre 2020 et commentée sur le blog de l’ineffable Scott Aaronson.
Alors que les scientifiques chinois se contentent prudemment de parler d’avantage quantique, certains médias comme ScienceNews n’hésitent pas à utiliser le vocable de suprématie quantique, comme dans The new light-based quantum computer Jiuzhang has achieved quantum supremacy par Emily Conover publié dans l’Américain ScienceNews.
Il n’a pas la même signification. Un point de sémantique est donc nécessaire :
- Un avantage quantique est observé avec un calculateur quantique lorsqu’il réalise une opération en un temps meilleur que les supercalculateurs les plus performants exploitant l’algorithme classique le plus efficace du moment. Meilleur, mais pas forcément de plusieurs ordres de grandeur.
- Une suprématie quantique intervient si un calcul quantique spécifique n’a pas d’équivalent classique exécutable dans un temps humainement raisonnable. Il vaut mieux que ce temps soit complètement déraisonnable, du genre de quelques milliers, millions voire milliards d’années. Au-delà de quelques semaines, ces temps de calcul sont bien entendu des estimations et des extrapolations. Il faut noter que l’on ne peut pas parler de suprématie quantique générique. Elle l’est au cas par cas, application par application et sur une machine clé. Le terme de suprématie est par ailleurs remis en question pour sa connotation politique, surtout aux USA.
En l’occurrence, l’expérience chinoise a l’air de relever sur le papier de la suprématie : le calcul quantique dure 200 secondes alors que son équivalent classique durerait 2,5 milliards d’années sur le Sunway TaihuLight, le supercalculateur le plus rapide en Chine et le quatrième au monde dans le classement TPC500. La différence de temps de calcul de cet échantillonnage entre simulation classique et calcul quantique est de 1014, ce qui nous fait 100 trillions au sens anglo-saxon avec un trillion = 1012. En français et dans le système international d’unités, un trillion = 1018, soit un million au cube. Sur la suggestion de Scott Aaronson qui faisait partie du comité de relecture du papier scientifique de Science, l’équipe chinoise a même simulé numériquement l’expérience jusqu’à 40 photons, consommant l’équivalent de $400K de puissance de calcul de supercalculateur. Jiuzhang serait aussi 10 milliards de fois plus rapide que les 53 qubits de Google Sycamore selon cette source sachant que Sycamore n’a jamais servi à faire de l’échantillonnage de bosons. Donc, pas évident de savoir comment ce ratio a-t-il pu être évalué.
Si d’un point de vue photonique, l’expérience chinoise est très impressionnante et consolide de nombreuses prouesses techniques, le calcul qu’elle réalise ne sert à rien en l’état. Un calcul quantique utile d’un point de vue pratique serait la résolution d’un problème d’optimisation, une simulation moléculaire ou une factorisation de nombre entier, qui sont trois grandes classes établies du calcul quantique. Il est trop tôt pour en voir la couleur.
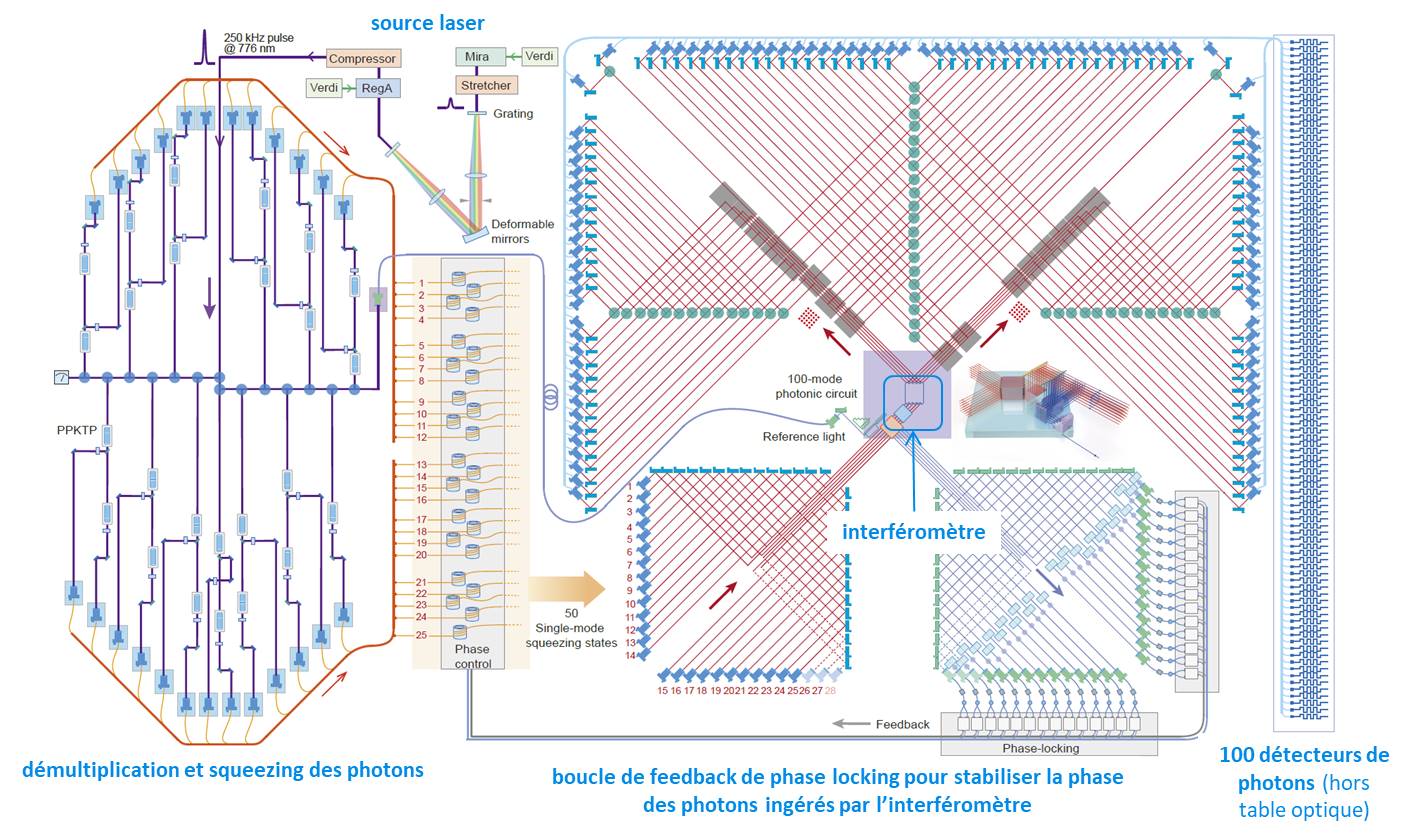
L’expérience chinoise est un échantillonnage de boson gaussien (GBS pour les intimes : gaussian boson sampling). Elle utilise la lumière d’un puissant laser qui alimente 25 cristaux qui dédoublent les photons (devenant donc 50 photons, moitié de phase horizontale et moitié verticale). Ces 50 photons sont injectés dans un interféromètre à trois dimensions fait en deux parties comportant respectivement 5 et 10 pièces en cristal (ci-dessous).
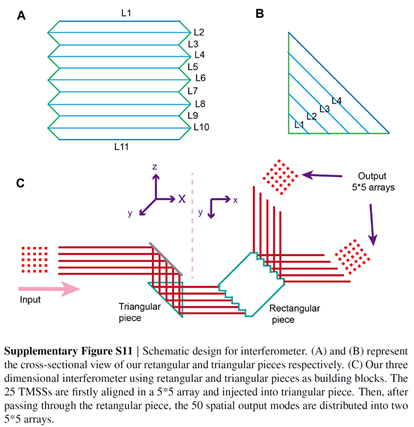
L’interféromètre applique mathématiquement une double opération matricielle unitaire de 50×50 aux photons entrants, une pour ceux de chaque phase (horizontale et verticale). Puis un séparateur de faisceau polarisant (PBS : Polarizing Beam Splitter) mélange les deux matrices pour donner une matrice unitaire de 100×100 qui alimente alors 300 prismes et 75 miroirs et en bout de course 100 détecteurs de photons originaires de la startup américaine Quantum Opus.
En algèbre linéaire, la principale branche des mathématiques utilisée en physique quantique, une matrice unitaire est une matrice carrée de nombres complexes qui donne une matrice “identité” lorsqu’elle est multipliée par sa matrice adjointe.
La génération des photons exploite de l’optical squeezing (compression optique) qui sert à améliorer la précision d’une caractéristique physique des photons générés par le système laser, comme la fréquence au détriment de la phase, en tirant parti du fameux principe d’indétermination d’Heisenberg. C’est une technique qui est testée dans les instruments de la collaboration américano-européenne LIGO-VIRGO qui servent à observer les ondes gravitationnelles.
L’instrument Jiuzhang est une sorte de grand mélangeur de photons. Il détecte en moyenne 43 photons, avec un maximum observé de 76 photons. Il n’intervient que de manière sporadique du fait des imperfections du système de génération de photons du système. Un véritable avantage peut être revendiqué à partir de d’une petite quarantaine de photons et est donc manifeste avec 76. Le record précédent de GBS était de 5 photons mesurés, également réalisé par les équipes de Jian-Wei Pan en avril 2019. L’information générée par l’instrument est une probabilité de distribution des photons sur les détecteurs.
L’impressionnant dispositif tient sur une table optique de trois mètres carrés (ci-dessus) sachant qu’une partie de l’appareillage est autour, ne serait-ce que les sources et amplificateurs laser (Coherent Mira 900, Verdi G et RegA 9000). La génération de la lumière laser en amont de l’expérience passe par plusieurs appareils en série. Pour le fun, ils la calibrent avec un analyseur de spectre et phase de lumière Swamp Optics GRENOUILLE, originaire de Géorgie (USA). En pratique, les photons générés dans l’expérience ne sont pas tous véritablement indistingables et parfaits.
Les détecteurs de photons sont refroidis à 2,5K. Ce refroidissement utilise des cryostats pas très encombrants, faisant environ 2 décimètres-cubes, mais complétés par un compresseur de forme cubique faisant environ 40 cm de côté. Ces systèmes de détection installés dans des racks peuvent accueillir 16 fibres en entrée (ci-dessous) et consomment chacun un total de 3 kW. Ce qui nous fait une consommation totale d’au moins 18 kW rien que pour les détecteurs de photons. Ces racks ne sont ni plus ni moins encombrants que les actuels systèmes de génération et d’analyse de micro-ondes qui sont placés à l’extérieur des cryostats des calculateurs quantiques à qubits supraconducteurs comme ceux d’IBM et Google.
La totalité des détecteurs doit occuper un rack et demi en tout. La consommation des lasers et amplificateurs de lasers doit ajouter quelques kW. Combien coûte l’ensemble de ce dispositif ? Au vu des prix publics des détecteurs de photons, des lasers et du reste, je dirais qu’à la louche il représente aux alentours de $2M, à confirmer par des experts en photonique. Ce n’est pas un montant extraordinaire. Il n’est en tout cas pas accessible qu’aux Chinois ! Il faut ajouter les $400K de la simulation et, bien évidemment, les coûts humains de l’expérience qui a bien du occuper quelques doctorants.
Simuler numériquement cette expérience physique sur un calculateur classique requiert une puissance de calcul qui augmente plus rapidement que l’exponentielle du nombre de photons mesurés en bout de course. Dans l’échantillonnage de bosons classique, il faut calculer des permanents de grandes matrices qui sont carrées. On doit la notion de permanent au mathématicien français Louis Cauchy en 1812. La formule ci-dessous en décrit le contenu.
Le П du permanent dénote une multiplication de valeurs de la matrice d’indices i et σ(i). σ est une fonction de permutation des entiers compris entre 1 et n, la dimension de la matrice (nombre de colonne et de lignes). Le sigma porte sur l’ensemble des fonctions σ du groupe des permutations Sn (dénommé aussi groupe symétrique) qui fait une taille de n! (factorielle de n). Les valeurs ai,σ(i) sont les cases de la matrice de coordonnées i et σ(i). Le schéma indique ce que cela donne avec n=2 et n=3 sachant qu’au-delà, cela devient moins lisible ! Le permanent est donc un nombre réel qui résulte de n! (factorielle de n) additions de multiplications de n valeurs de la matrice. Le temps de calcul du permanent d’une matrice carrée de n lignes et colonne est plus qu’exponentiel en fonction de n. C’est un problème dit “NP-difficile” dans la théorie de la complexité. Notre n correspond ici au nombre de photons qui rentrent dans l’interféromètre. Un permanent doit être calculé pour évaluer toute probabilité d’obtenir une combinaison de photons donnée dans les détecteurs. Dans l’expérience, l’injection de photons est réalisée un grand nombre de fois et l’apparition des photons dans les détecteurs moyennée. On a donc une vision probabiliste de l’effet de l’interféromètre, ce qui est le propre de tout calcul quantique.
Dans l’échantillonnage de boson gaussien (les photons sont un type de boson), on utilise des torontoniens qui sont des modèles mathématiques dérivés des permanents. Ces torontoniens sont décrits dans Gaussian boson sampling using threshold detectors par Nicolás Quesada, Juan Miguel Arrazola et Nathan Killoran, 2018 (9 pages). Surprise, ce sont des chercheurs basés à Toronto ! Le papier dit que “the Torontonian can be interpreted as an infinite sum of Hafnians.”. Qu’est-ce qu’un hafnien ? Pour faire simple, c’est une variante plus compliquée et plus lourde à calculer des permanents ! Je vous passe les détails, et lorsque je dis ça, c’est que je n’ai pas encore compris (formules ci-dessous, détaillées dans le papier cité dans le paragraphe)!
J’en déduis en tout cas une méta-information : comme le GBS est plus compliqué à simuler numériquement qu’un échantillonnage de bosons classique, il permet d’en mettre encore plus plein les mirettes dans la comparaison avec le calcul classique.
Le papier chinois évoque des publications de cas d’usages concrets de l’échantillonnage de boson gaussien en gestion de graphes et simulations moléculaires. Il cite Using Gaussian Boson Sampling to Find Dense Subgraphs par Juan Miguel Arazola (le même que celui des hafniens et des torontoniens) et Thomas Bromley, 2018 (6 pages) et Boson Sampling for Molecular Vibronic Spectra par Alán Aspuru-Guzik et al, 2014 (10 pages). Ce dernier papier ne fait cependant pas référence au GBS (gaussian boson sampling). Il y a aussi Molecular docking with Gaussian Boson Sampling par Leonardo Banchi et al, juin 2020 (10 pages), sur de la simulation d’amarrage moléculaire, utile en conception de thérapies innovantes.
Notez au passage que l’interféromètre de l’expérience chinoise tout comme le reste de l’instrumentation utilisée sont statiques et donc, l’expérience qui va avec aussi. Ce n’est donc pas encore un appareil programmable avec des paramètres en entrée (un graphe, whatever) et un résultat en sortie (comme un parcours optimum dans un graphe). Comment se ferait alors le paramétrage du système ? On peut visiblement le faire en préparant de manière différenciée l’état des photons “squeezés” (compressés) qui alimentent l’interféromètre. Le procédé est décrit dans Gaussian Boson Sampling for perfect matchings of arbitrary graphs par Kamil Bradler et al (encore de Toronto…), décembre 2017 (17 pages). L’avantage serait-il le même dans ces conditions ? Scott Aaronson en doute beaucoup.
Dans le cas de la suprématie de Google, on voyait bien la différence entre l’expérience de suprématie publiée en octobre 2019 portant sur un algorithme utilisant pleinement 53 qubits sur une 20 séquences aléatoires de portes quantiques et ce qui a suivi. Les papiers publiés en avril 2020 sur de la simulation moléculaire ou la résolution de problèmes d’optimisation se contentaient d’utiliser entre 12 et 23 qubits des 53 de la puce Sycamore. Ils perdaient tout avantage ou suprématie quantique au passage ! Le passage à l’utile est donc semé d’embûches. Voir Quantum Approximate Optimization of Non-Planar Graph Problems on a Planar Superconducting Processor, avril 2020 (17 pages) qui porte sur trois familles de problèmes de combinatoire avec l’algorithme QAOA et Hartree-Fock on a superconducting qubit quantum computer, avril 2020 (27 pages) sur un algorithme de simulation moléculaire d’une molécule comportant quatre atomes.
Au même titre que n’importe quel processus physique, chimique ou biologique naturel qui est toujours plus compliqué à simuler numériquement qu’à laisser fonctionner naturellement, il est normal qu’un outil manipulant des photons soit plus efficace qu’un outil qui simule numériquement les interactions entre les photons. On pourrait utiliser l’analogie du verre d’eau. Aucun ordinateur quantique ou classique n’est capable de simuler à l’atome près ce qui se passe dans un verre d’eau. Le verre d’eau ne réalise cependant aucun calcul utile. Bref, simuler physiquement un processus physique aléatoire ne génère pas forcément d’information exploitable.
Il y a un autre lézard. Les comparaisons de suprématie entre calcul quantique et simulation numérique de ce calcul sont en fait souvent biaisées. Dans la version numérique, le calcul est effectué de manière déterministe et avec précision. Dans les versions quantiques actuelles, autant chez Google que chez les Chinois, le calcul est bruité et donc imprécis. Or, on peut émuler un calcul bruité avec beaucoup moins de ressources qu’un calcul exact… semble-t-il sur un simple PC ! C’est ce qui ressort du papier What limits the simulation of quantum computers? publié récemment dans Physical Review Letters par Yiqing Zhou, E. Miles Stoudenmire et Xavier Waintal, ce dernier étant du laboratoire IRIG du CEA à Grenoble. Ils ont fait la comparaison en s’appuyant sur l’expérience de Google d’octobre 2019.
Pour résumer, l’expérience chinoise constitue une grande avancée en photonique. Elle ouvre probablement la porte à des progrès dans le calcul quantique sachant que ceux-ci vont demander encore plus d’efforts aussi bien en photonique qu’en algorithmie. Il faut enfin noter que l’exercice de style de l’échantillonnage de bosons est une expérience particulière de photonique. Les Chinois s’en sont fait une spécialité. En Europe, c’est notamment celle du chercheur Fabio Sciarrino de l’Université Sapienza de Rome.
D’autres travaillent sur du calcul quantique avec des méthodes plus génériques. On peut notamment compter avec PsiQuantum, Orca Computing, QuiX et Quandela (avec ses sources de photons indistingables de qualité) qui ambitionnent tous de créer des accélérateurs quantiques programmables à base de qubits photons.
Les éléments de performance du calcul quantique
L’expérience chinoise récente illustre bien le besoin de disposer d’outils d’évaluation des capacités pratiques des calculateurs ou accélérateurs quantiques. J’utilise l’une ou l’autre des appellations. La notion d’accélérateur vient du fait qu’un calculateur quantique est toujours exploité comme un coprocesseur d’un calculateur classique et très souvent avec des algorithmes dits hybrides qui associent une part de calcul classique interagissant avec une part de calcul quantique.
Pourquoi vouloir benchmarker les calculateurs quantiques ? Cela a au moins deux intérêts : comparer les accélérateurs ou calculateurs quantiques entre eux et évaluer leur performance relative vis à vis des meilleurs supercalculateurs du marché.
Les comparaisons portent généralement sur le temps de calcul. Elles pourraient aussi concerner d’autres paramètres des machines comparées : leur consommation d’énergie pour le calcul donné, leur poids et encombrement ainsi que leur coût. Aujourd’hui, on se contente de comparer les temps de calcul mais lorsque les machines seront industrialisées, les comparaisons deviendront certainement multifactorielles. Ne serait-ce que pour apprécier plus largement les bénéfices du calcul quantique au-delà du temps des opérations.
Quelles sont les caractéristiques clés d’un ordinateur classique ? Rien que pour le calcul, on évalue la puissance en opérations par secondes. Ces opérations portent sur des nombres entiers ou flottants d’une certaine taille en bits. Ainsi, on peut parler de 100 TFLOPS/s obtenus avec des calculs en nombres flottants stockés sur 16 bits. La puissance d’un supercalculateur dépend d’autres paramètres : sa mémoire vive, sa connectique réseau dans les serveurs et entre serveurs, et sa capacité de stockage, avec à chaque fois leurs débits et latences.
Pour un calculateur quantique, on évoque rarement les TFLOPS (flottants) ou même TOPS (entiers) même si on peut réaliser des calculs flottants ou entiers à partir de portes quantiques et les paralléliser massivement. La puissance du calcul quantique vient surtout de l’intrication des qubits entre eux et de phénomènes d’interférences qui ne s’expriment pas facilement en opérations par secondes, ce d’autant plus que ce sont des mécanismes que l’on pourrait qualifier d’analogiques.
On s’intéresse généralement au nombre de qubits, à leur fidélité ainsi qu’à leur connectivité. Plus cette dernière est grande, moins on aura besoin de portes quantiques pour relier les qubits entre eux et plus rapide sera le calcul. La fidélité est souvent évaluée en % (100% – le % d’erreurs) pour les portes à un qubit, à deux qubits et la fidélité de la mesure des qubits. Mais cette fidélité dépend du nombre de qubits utilisés dans un processeur donné. Plus on utilise de qubits, plus elle baisse, en tout cas pour les qubits supraconducteurs et à ions piégés. On peut aussi s’intéresser à la vitesse d’horloge du calcul quantique : à quelle fréquence les portes quantiques sont-elles exécutées ? C’est un paramètre rarement évoqué mais il est important. Certains le négligent du fait de l’accélération dite exponentielle du calcul quantique. En pratique et pour pas mal d’algorithmes, l’accélération obtenue n’est que polynomiale et donc moins impressionnante. Ce qui veut dire que la vitesse d’exécution des portes quantique peut jouer un rôle dans la performance du calculateur.
Ce qui compte donc en tout cas en ce moment est surtout la capacité à exécuter les calculs sur un certain nombre de qubits et avec une série de portes quantiques qui ne généreront pas d’erreurs préjudiciables au bon résultat.
Le volume quantique d’IBM
IBM communique depuis 2017 sur la notion de volume quantique pour évaluer la puissance de ses calculateurs quantiques. Cette notion a été reprise par Honeywell en mars 2020 puis par IonQ en octobre 2020.
Le volume quantique est un nombre entier censé associer la quantité de qubits et le nombre de portes quantiques qui peuvent être exécutées consécutivement sans que les erreurs qui s’accumulent soient préjudiciables à la précision des calculs. IBM indiquait ainsi les configurations de qubits leur ayant permis de passer d’un volume quantique de 4 avec 5 qubits en 2017 à 32 en mars 2020 puis à 64 en août 2020, avec 28 qubits.
C’est en apparence très simple. Mais dès que l’on cherche à comprendre d’où vient ce nombre magique, les choses se compliquent. Ce volume quantique est évalué via un benchmark de calcul aléatoire consistant à enchaîner des portes quantiques aléatoires et qui doit donner un résultat correct dans deux tiers des cas. Pourquoi deux tiers ? Parce que le calcul quantique fournit un résultat probabiliste. Pour obtenir un résultat déterministe, on exécute le calcul plusieurs fois et on évalue la moyenne des résultats, jusqu’à des milliers de fois comme c’est proposé par IBM dans son système en cloud. Avec une moyenne de bons résultats aux deux tiers, on peut donc statistiquement converger vers un bon résultat au bout de quelques mesures. La précision du résultat va dépendre de ce nombre.
Dans la première définition de 2017 du volume quantique, dans Quantum Volume de Lev Bishop, Sergey Bravyi, Andrew Cross, Jay Gambetta et John Smolin, 2017 (5 pages), il s’agissait du nombre maximum de qubits sur lequel le processeur pouvait effectuer ce calcul, élevé au carré. Pourquoi ce carré était-il alors appelé un volume ? Parce qu’IBM expliquait qu’il dépendait de trois paramètres : le nombre de qubits, le nombre de séquences de portes quantiques enchaînables et la connectivité des qubits. Trois paramètres, donc trois dimensions, donc un cube. Sauf que la formule était un carré… !
La définition a évolué ensuite en 2019 pour devenir 2 à la puissance de ce nombre de qubits, qui n’est donc pas plus un cube qu’avant. Elle est documentée dans Validating quantum computers using randomized model circuits par Andrew W. Cross et al, 2019 (12 pages).
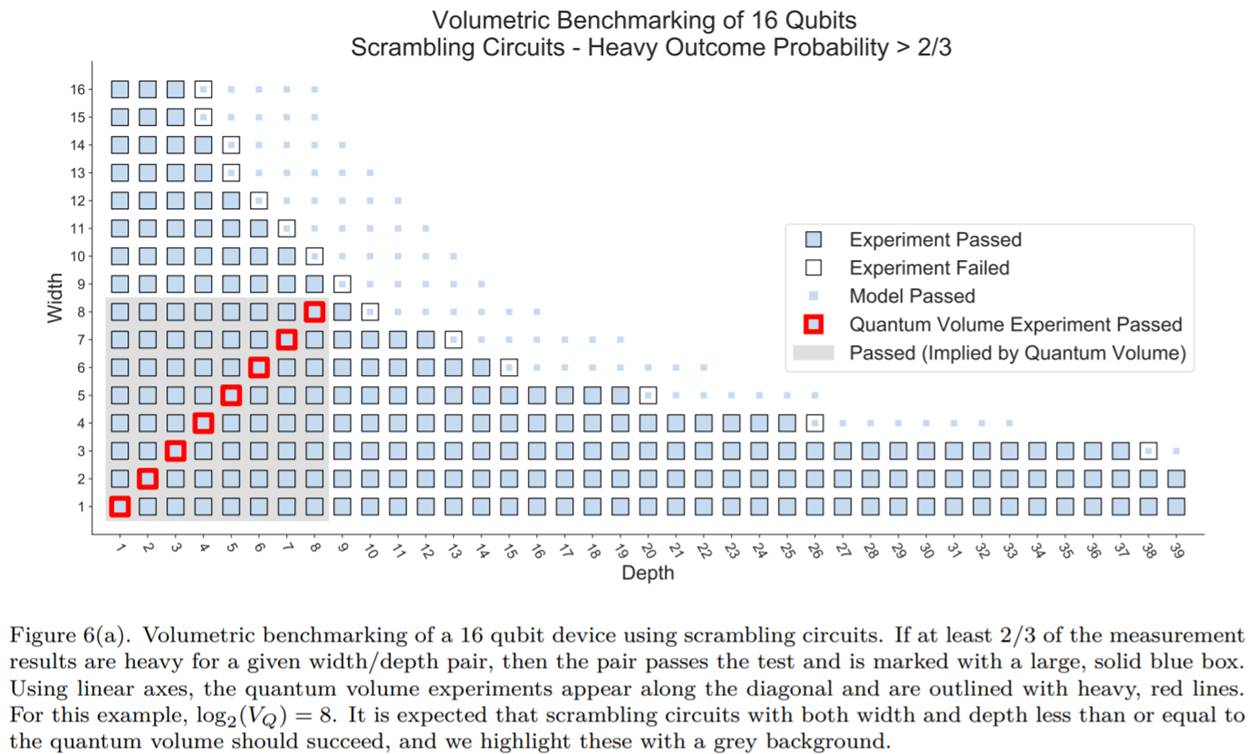
Le schéma ci-dessus explique la manière dont les volumes quantiques de 2017 et 2019 sont évalués. Le schéma ci-dessous issu d’un document de Robin Blume-Kohout et Kevin Young (voir A volumetric framework for quantum computer benchmarks, février 2019, 24 pages) précise la manière dont le m (nombre de qubits) et le d (profondeur de calcul) sont évalués.
Dans l’exemple ci-dessous, le nombre de qubits obtenu pour évaluer le volume quantique est inférieur au nombre total de qubits du processeur, 8 pour 16 dans ce cas. Le benchmark ne permet d’enchaîner que 8 séries de portes quantiques d’affilée sur 8 qubits, pour 38 avec seulement deux qubits. Dans sa version 2017, le volume quantique est la surface du carré en gris contenant les carrés entourés de rouge.
Dans sa version 2019, il devient 28, soit 256 au lieu de 64 (8×8). Ce n’est finalement que la taille de l’espace de Hilbert opérationnel du calculateur, soit le nombre d’état superposés différents qu’il est capable de gérer d’un point de vue pratique avec une profondeur de calcul égale au nombre des qubits correspondants.
Lorsqu’IBM annonce qu’un calculateur de 28 qubits atteint un volume quantique de 32, cela veut dire qu’ils n’arrivent à valider leur benchmark qu’avec 5 qubits parmi ces 28 qubits. Pour sa part, l’annonce d’IonQ d’un volume quantique supérieur à quatre millions correspond à 222, précisément 4 194 304.
Donc, à la capacité d’exécuter 22 séries de portes quantiques sur 22 des 32 qubits du processeur à ions piégés qu’ils ont annoncé en octobre 2020, avec deux tiers de résultats corrects sur le benchmark aléatoire utilisé. Ce record, pas encore bien documenté, semble lié à la bonne connectivité des qubits des ions piégés. Ceux-ci peuvent être ainsi tous intriqués directement les uns avec les autres contrairement aux qubits supraconducteurs qui sont, au mieux, intriquables qu’avec leur voisin immédiat. Cela permet de réaliser le benchmark en moins de séries de portes quantiques que sur des qubits supraconducteurs, qui requièrent beaucoup de portes SWAP générant des erreurs qui s’accumulent rapidement.
Le volume quantique est limité à une cinquantaine de qubits opérationnels. En effet, il ne peut être évalué qu’avec un benchmark comparant les qubits avec leur émulation sur un calculateur classique. Or, celle-ci est contrainte par la taille mémoire de ces derniers, qui atteint ses limites entre 50 et 55 qubits.
A quoi bon donc évaluer la puissance d’un calculateur quantique que dans le cas où celle-ci est inférieure à celle des supercalculateurs ? Qui plus est, IBM s’est fait piéger par son propre benchmark. Ils annoncent qu’ils vont doubler leur volume quantique tous les ans. En pratique, cela revient à ajouter un qubit opérationnel par an. Et là, ils sont en retard de 14 ans par rapport à IonQ ! Tout cela semble incohérent avec leur objectif affiché de plus que doubler le nombre de qubits supraconducteurs par an (65 en 2020, 127 en 2021, 433 en 2022 et 1121 en 2023 puis un million bien au-delà de 2024).
Le Q-score d’Atos
Là-dessus intervient l’intéressant benchmark Q-score annoncé par Atos vendredi 4 décembre 2020 dans un webinar avec la participation d’Elie Girard (CEO d’Atos), Cyril Allouche (responsable R&D quantique d’Atos) et les membres du conseil scientifique quantique d’Atos Serge Haroche, Alain Aspect, Daniel Estève, Artur Ekert et David DiVincenzo.
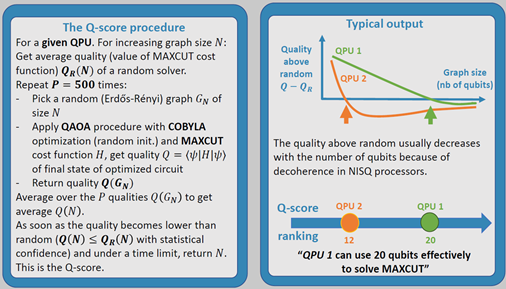
Au lieu de comparer la puissance de calcul, le Q-score consiste à évaluer la taille d’un problème classique qui peut être résolu avec la machine évaluée. Le sujet retenu est celui du MaxCut, un problème de combinatoire classique dans le calcul quantique. On le retrouve dans la résolution de problèmes comme celui du voyageur de commerce. Il a des applications dans tout un tas de domaines et métiers comme dans la logistique, l’industrie ou la finance. On peut aussi l’exploiter pour faire du clustering, la méthode principale du machine learning non supervisé visant à découvrir de nouvelles classes d’objets. Le benchmark Q-score est calculé en faisant appel à un algorithme hybride classique+quantique de type QAOA (Quantum Approximate Optimization Algorithm), voir le schéma ci-dessous qui en explique le principe.
Les avantages de cette approche sont nombreux : le métrique est simple (le nombre de variables du problème d’optimisation), il est indépendant de l’architecture des qubits et surtout, il ne nécessite pas d’émulation du calcul quantique sur calculateur classique. On peut en effet vérifier que les solutions générées sont valides avec un calcul classique.
Atos a décidé de publier lui-même quelques benchmarks de calculateurs quantiques du marché, réalisés avec ses propres machines d’émulation aQML qui peuvent traiter jusqu’à 41 qubits. Ils pourraient aussi exécuter leur benchmark sur les accélérateurs quantiques facilement accessibles, en particulier dans le cloud, tout comme par n’importe quel utilisateur. A ce jour, les meilleurs résultats sont situés autour de 15Q (donc, 15 variables pour un problème d’optimisation). Ces benchmarks sont réalisés sur des machines NISQ, à savoir des accélérateurs quantiques “bruités” (où les qubits ne sont pas corrigés). La supériorité quantique sera atteinte avec un Q-Score situé aux alentours de 60Q. On verra s’il est possible ou pas de l’obtenir avec du NISC où s’il faudra attendre de disposer d’accélérateurs à tolérance de pannes corrigés (dits LSQC, large scale quantum computers).
Ce type de benchmark devra probablement être complété par un à deux autres benchmarks qui s’appliquent à d’autres domaines d’application du calcul quantique : l’un pour la simulation chimique, exprimé éventuellement en nombre d’atomes de molécule simulable, et l’autre concernant la taille (en puissance de deux, les clés RSA étant de taille évaluée en nombre de bits comme 1024 ou 2048) d’un entier factorisable. Nombre de ces benchmarks n’auront de sens qu’avec des calculateurs scalables à tolérance de pannes (LSQC).
Pour ce qui est de la simulation chimique, le laboratoire Oak Ridge du Département de l’Energie US a proposé un benchmark. Voir ORNL researchers advance performance benchmark for quantum computers, janvier 2020. Celui-ci porte sur trois molécules à deux atomes (NaH, KH et RbH) qui sont accessibles aux calculateurs quantiques existants d’IBM et Rigetti de 20 et 16 qubits. Il ne présente pas la généricité du Q-score d’Atos pour aller au-delà de cette taille de molécules. C’est peut-être cela qui explique le fait qu’Atos n’ai pas intégré cela. Il faudrait définir une série de molécule de taille croissante ou créer des molécules artificielles, qui n’auraient pas forcément de valeur applicative.
On a aussi le “cycle benchmarking” présenté dans Characterizing large-scale quantum computers via cycle benchmarking par Alexander Erhard et al., 2019 (7 pages), issu d’une équipe associant le Canada, le Danemark et l’Autriche et qui évalue à bas niveau la qualité de l’intrication des qubits.
Reste pour Atos à faire adopter et donc à marketer ce Q-score. Le fait de démarrer en publiant quelques benchmarks par eux-mêmes permet de “boostraper” leur modèle. Il faut ensuite jouer sur le phénomène du me-too pour que les autres l’adoptent. Notamment les laboratoires et startups qui n’ont pas encore mis leur accélérateur quantique en libre-service dans le cloud.
Par certains côtés, cette initiative fait penser au DXOmark. Il s’agit d’un benchmark de capteurs photos proposé par l’éditeur français de logiciel de dérushage RAW DXO. Ils benchmarkent régulièrement la sensibilité des capteurs d’appareils photos de toutes catégories, ceux des smartphones compris. Cela contribue à leur notoriété dans le marché de la photo numérique. Ici, le benchmark d’Atos permet de faire le comarketing de leur émulateur matériel et logiciel aQML, déjà bien commercialisé dans le monde au Japon, aux USA, en Allemagne, en Finlande, au Royaume-Uni et en France, ainsi que leur langage de programmation AQASM et l’environnement de développement myQLM qui permet de l’exécuter sur son propre micro-ordinateur.
Pour éviter de réaliser tous les benchmarks, Atos a prévu de publier les outils logiciels du Q-score en open source d’ici début 2021. C’est une bonne initiative. Elle pourrait être prolongée par la création d’une structure associative de consolidation des résultats, par exemple sous la coupe d’une grande Université. Il serait aussi intéressant de faire adopter le benchmark par des laboratoires de recherche de pointe, comme ceux de Jian-Wei Pan qui sont à l’origine de ces records d’échantillonnage de bosons. Et la boucle narrative de cet article serait ainsi bouclée !
À creuser !
![]()
![]()
![]()
Reçevez par email les alertes de parution de nouveaux articles :
![]()
![]()
![]()




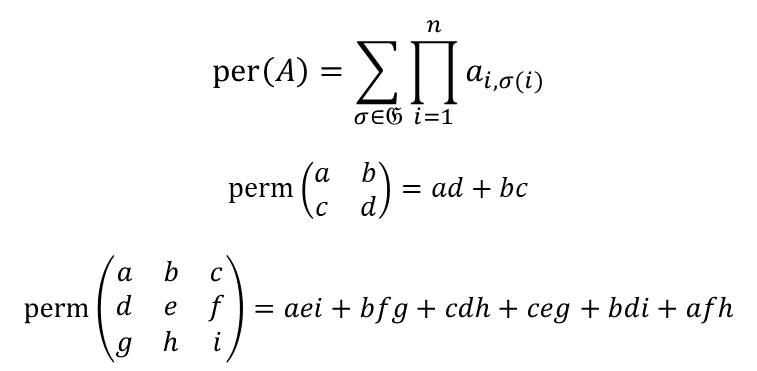
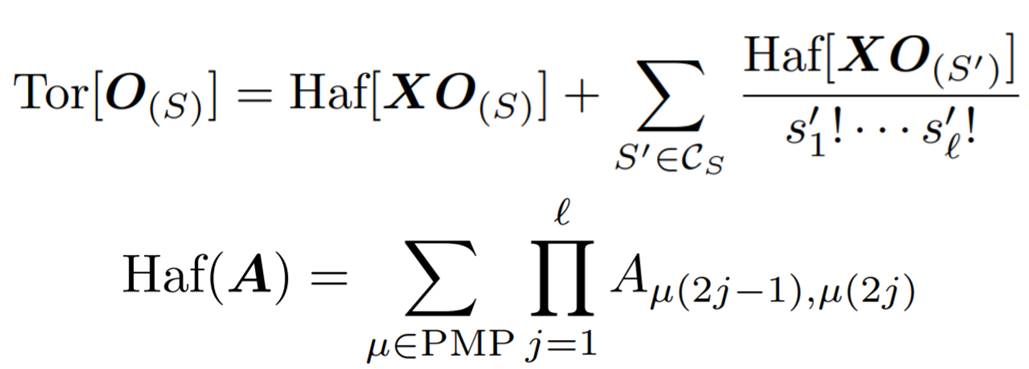






























 Articles
Articles
A very exhaustive post on the benchmarking of quantum computers (in French) “Comment benchmarker les calculateurs q… https://t.co/ketxaRdxlr
@JF_LEHE @dlouapre Merci, je vais regarder !
L’overview d’@olivez est hyper complet , et tout frais ! https://t.co/6uYOyxhZyL